Ableitung: Grundlagen und Steigung

In diesem Abschnitt präsentieren wir euch die Grundlagen zur Ableitung von Funktionen. Dabei klären wir, was es mit der Steigung auf sich hat. Zu diesem Zweck schauen wir uns zunächst eine lineare Funktion an.

Beginnt der Lehrer mit dem Thema Ableitung, findet sich oft irgend eine Funktion an an der Tafel, an der eine Sekante eingezeichnet wird. Dann kommen eine paar Sätze in denen die Wörter Sekante, Tangente und Steigung auftauchen.  Nach einigen Erklärungsversuchen des Lehrers sind die Schüler anschließend leider meist genauso schlau, wie vorher. Deshalb nähern wir uns dem Problem nun einmal ganz langsam an.

Konstante Steigung

Schaut euch einmal die folgende Grafik an: Dort seht ihr eine Funktion eingezeichnet. Ziel ist es, deren Steigung zu bestimmen. Steigung? Nun das kennt eigentlich jeder. Ihr steht vor einer Straße, die den Berg hoch geht. Ihr habt also eine Steigung zu bewältigen. So etwas kann man auch mathematisch beschreiben. Also erst einmal  die Grafik ansehen, darunter gibt es dann einige Erklärungen.

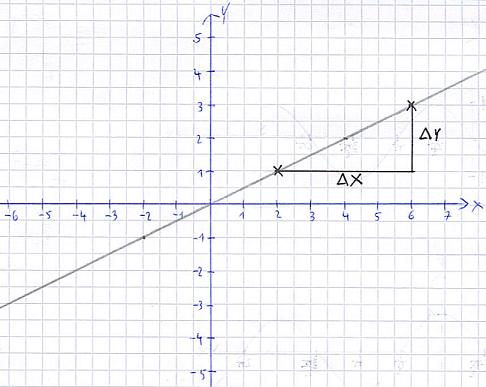
Erklärungen: Wie ihr sehen könnt, ist die Steigung überall gleich. Diese möchten wir nun ausrechnen. Dabei wählen wir uns zwei Punkte und bilden dann ein Steigungsdreieck. Hier eine Schritt-für-Schritt Anleitung:

• Wählt einen ersten Punkt auf der Gerade aus. Punkt 1: x = 6 und y = 3
• Wählt einen zweiten Punkt auf der Gerade aus: Punkt 2: x = 2 und y = 1
• Bildet Δy durch Subtraktion der y-Angaben: 3 - 1 = 2
• Bildet Δx durch Subtraktion der x-Angaben: 6 - 2 = 4
• Steigung = Δy : Δx -> Steigung = 2 : 4 = 0,5
• Die Steigung beträgt somit 0,5

Die Steigung ist überall gleich. Das macht es recht einfach, diese zu berechnen. Aufwendiger wird es, wenn ihr eine "krumme" Funktion habt und das Steigungsverhalten analysieren wollt. Genau darum dreht sich die Differentialrechnung. Dies schauen wir uns im nun Folgenden an.

Nicht konstante Steigung

Soeben hatten wir uns mit der Steigung einer linearen Funktion beschäftigt. Diese war überall gleich. Jetzt schauen wir uns das Steigungsverhalten einer nichtlinearen Funktion einmal an. Was zunächst auffällt: Die Steigung ist nicht überall gleich. Aber seht euch dies zunächst erst einmal selbst an:

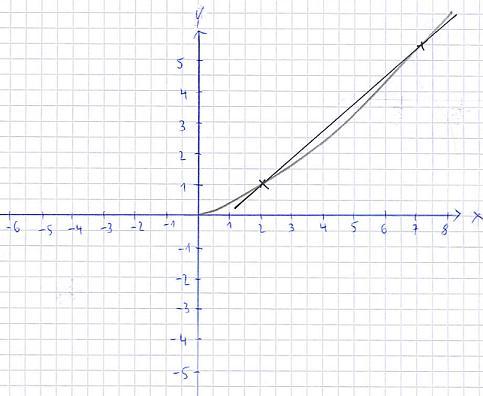
Erklärungen: Wir wollen nun die Steigung in einem gewissen Punkt rausfinden. Nehmen wir uns dazu den Punkt x = 2 und y = 1, den ich durch ein kleines Kreuzchen in der Grafik eingezeichnet habe. Um ein Steigungsdreieck zu erhalten wird ein zweiter Punkt eingetragen ( so wie wir das auch bei der linearen Funktion gemacht haben ), in diesem Fall bei x = 7 und y = 5,5. Verbinden wir diese beiden Punkte haben wir eine Sekante, sprich die Funktion wird an zwei Stellen geschnitten ( dort wo die Berührpunkte mit der eingezeichneten Gerade liegen ). Mit dieser könnten wir eigentlich jetzt die Steigung berechnen, eigentlich...

Denn leider haben wir einen kleinen Fehler gemacht. Schaut man sich die Gerade einmal an, sieht man, dass diese nicht ganz der Steigung im Punkt x = 2 und y=1 entspricht. Der Grund: Die Funktion, die wir haben, ist gekrümmt und ändert ständig die Steigung. Nehmen wir uns also einen zweiten Punkt in etwas größerer Entfernung zum ersten Punkt, entsteht eine "ungenaue" Steigung. Deshalb müssen wir den zweiten Punkt ganz nah am ersten Punkt wählen. Schieben wir diesen zweiten Punkt ganz nah an den ersten ran, haben wir irgendwann den Punkt erreicht, wo der eine Punkt fast auf dem zweiten Punkt liegt. Wir haben dann nur noch einen Schnittpunkt mit der Geraden und damit eine Tangente mit exakter Steigung vorliegen.

Die Differentialrechnung

Die Differentialrechnung untersucht das Steigungsverhalten. Schülern wird manchmal die Herleitung erspart oder nur in kurzer Zeit gezeigt. Was ihr euch merken müsst: Durch das Ableiten einer Funktion erhaltet ihr deren Steigungsverhalten. Um dies möglichst einfach zu machen, braucht ihr euch nicht mit Grenzwertübergängen zu quälen, sondern müsst "nur" einige Ableitungsregeln kennenlernen. Mit genau diesen befassen wir uns in den folgenden Artikeln. Dabei gilt: f(x) = ... bzw. y = ... stellt die "Ausgangsfunktion" dar. Leitet man ab, erhält man f'(x) = ... bzw. y' = .... Leitet man noch einmal ab, erhält man f''(x) = ... bzw. y'' = .... Dazu mehr in den nächsten Artikeln.

Links:

• Ableitungsregel: Faktorregel und Summenregel
• Zurück zur Ableitung-Übersicht
• Zur Mathematik-Übersicht