Matrizen multiplizieren

Das multiplizieren eines Skalars mit einer Matrix sowie die Multiplikationen vom Matrizen miteinander werden in diesem Artikel der Mathematik näher behandelt. In diesem Zusammenhang erläutern wir euch auch das Falk-Schema.

Bevor wir die Multiplikation eines Skalars mit einer Matrix sowie die Multiplikation von Matrizen miteinander betrachten, solltet ihr sicher stellen, dass ihr die benötigen Vorkenntnisse habt. Dazu sollte euch klar sein, was eine Matrix überhaupt ist. Auch solltet ihr wissen, wie man Matrizen addiert und subtrahiert:

• Matrix und Matrizen: Grundlagen
• Matrix: Addition und Subtraktion

Matrix Multiplikation Video:
Dieser Artikel liegt auch als Video vor.

• Hinweise: Dies ist noch ein Tafelvideo. Eine Neuauflage in HD ist geplant. Der Abruf ist auch direkt in der Rubrik Matrix Multiplikation Video möglich.
• Probleme: Bei Abspielproblemen bitte den Artikel Video Probleme aufrufen.

Matrix: Multiplikation mit einem Skalar

Beginnen wir mit etwas ganz einfachem: Der Multiplikation einer Matrix mit einem Skalar. Die folgende Regel dazu solltet ihr euch merken: Eine Matrix wird mit einem Skalar multipliziert, indem man jedes Matrixelement mit dem Skalar multipliziert. Die beiden folgenden Beispiele zeigen euch, wie dies funktioniert. Dabei wird die Matrix A mit einer Zahl multipliziert und damit die Matrix B und C gebildet.

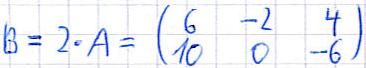
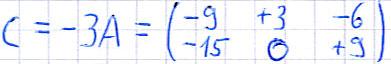
Aus den beiden Beispielen sollte das Prinzip leicht zu verstehen sein.

Multiplikation von Matrizen

In diesem Abschnitt beschäftigen wir uns mit der Multiplikation von zwei Matrizen. Berechnet werden soll die Matrix C = A · B. Die Elemente eines Matrizenproduktes werden als Skalarprodukte aus einem Zeilenvektor von A mit einem Spaltenvektor von B gebildet. Dies ist jedoch nur möglich, wenn beide Vektoren gleich viele Komponenten besitzen. Die Spaltenzahl von A muss mit der Zeilenzahl von B übereinstimmen.

Dies mag auf den ersten Blick etwas kompliziert wirken. Um eine solche Multiplikation zu vereinfachen, zeigen wir euch gleich das Falk-Schema. Das folgende Beispiel soll dessen Prinzip erläutern.

Die beiden Matrizen A und B sehen wie folgt aus:

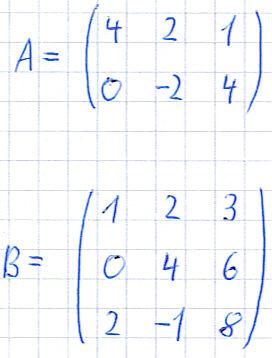
Um die Multiplikation du berechnen, wird das Falk-Schema eingesetzt. Dazu werden die Matrizen wie folgt hingeschrieben:

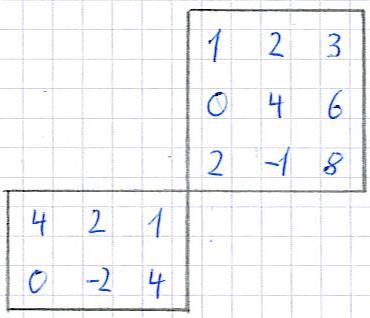
Nun wird gerechnet. Ich gebe euch zunächst einmal das Ergebnis an. Wie dies berechnet wird, steht unterhalb:

Die Berechnung erfolgt wie folgt:

• 4 · 1 + 2 · 0 + 1 · 2 = 6
• 4 · 2 + 2 · 4 + 1 · (-1) = 15
• 4 · 3 + 2 · 6 + 1 · 8 = 32
• 0 · 1 + (-2) · 0 + 4 · 2 = 8
• 0 · 2 + (-2) · 4 + 4 · (-1) = -12
• 0 · 3 + (-2) · 6 + 4 · 8 = 20

Leider ist die Berechnung relativ fehleranfällig. Aus diesem Grund muss man die Multiplikation und Addition sehr gründlich durchführen und dabei auch auf die Vorzeichen genau achten. Vertauscht man die Matrizen A und B ist die Multiplikation nicht mehr möglich. Wer es nicht glaubt, probiert es einfach einmal aus.

Links:

• Zur Mathematik Übersicht