Rechnen am Viereck

Das Rechnen am Viereck wird in diesem Artikel der Mathematik erklärt. Dabei zeige ich zunächst, worum es sich bei einem Viereck überhaupt handelt. Anschließend liefern wir euch Beschreibungen von verschiedenen Typen von Vierecken sowie passende Formeln für diese.

Um die folgenden Beschreibungen zu Vierecken zu verstehen, solltet ihr ein paar Vorkenntnisse aus dem Bereich der Mathematik mitbringen. Wem die folgenden Themen noch nichts sagen, der sollte diese erst einmal durchlesen. Alle anderen können gleich zur Definition des Vierecks weitergehen.

• Variablen und Formeln
• Strecken ( Geometrie )
• Winkel ( Geometrie )

Definition des Vierecks

Beginnen wir mit der Definition eines Vierecks: Eine ebene, von vier Strecken eingeschlossene Figur, heißt Viereck. Dabei bezeichnet man die vier Strecken als die Seiten des Vierecks. Liegen zwei Seiten aneinander, so haben sie einen gemeinsamen Eckpunkt. Diesen Eckpunkten werden meistens die groß geschriebenen Buchstaben A, B, C und D zugewiesen. Zu dem werden Winkel im mathematisch positivem Sinne in das Viereck eingezeichnet. Diese lauten α ( gesprochen: Alpha ), β ( gesprochen Beta ), γ ( gesprochen: Gamma ) und δ ( gesprochen: Delta ). Die Strecken, welche das Viereck bilden werden zu dem mit a, b,c und d bezeichnet.

Nutzt man die eben angegeben Bezeichnungen, kann man noch einige weitere Eigenschaften an dem Viereck sehen: Die Seiten a und c sowie b und d sind gegenüberliegende Seiten. Zu dem sind a und b, b und c, c und d sowie a und d benachbarte Seiten. Die Diagonalen das Vierecks erhält man, in dem man die gegenüberliegen Seiten jeweils miteinander verbindet. Auf diese Art und Weise erhält man die Strecke e zwischen A und C sowie die Strecke f zwischen B und D. Die folgende Grafik zeigt euch noch einmal das Viereck:

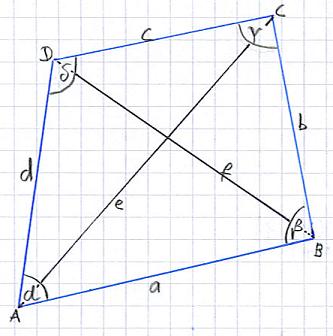
Eigenschaften des Vierecks:

• Umfang: Als Umfang des Vierecks wird die Summe aller Streckenlängen bezeichnet.
  • Umfang = a + b + c + d

• Winkelsumme: Addiert man die Summe aller Innenwinkel - siehe Grafik oben - erhält man 360 Grad, wie bei einem Kreis
  • Winkelsumme = 360º =α + β + γ + δ

• Information: Ein Viereck hat vier Ecken, vier Innenwinkel und vier begrenzende Strecken.

Konvex und Konkav:
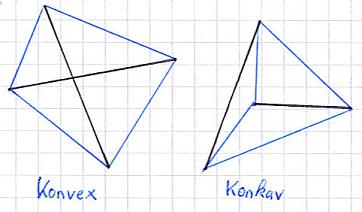
Man unterscheidet zwei verschiedene Arten von Vierecken: Konvexe und konkave. Liegen alle Diagonalen ( schwarz eingezeichnet ) innerhalb des Vierecks, wird es als konvex bezeichnet, ansonsten als konkav. Die folgende Grafik zeigt beide Fälle.

Typen / Klassifizierung von Vierecken

Es gibt eine ganze Reihe verschiedener Vierecke. Um die Länge dieses Artikels jedoch nicht zu sprengen, habe ich für die einzelnen Typen jeweils einen eigenen Artikel angelegt. Klickt auf die folgenden Links um den jeweiligen Artikel zu sehen:

• Rechteck
• Quadrat
• Parallelogramm
• Trapez
• Raute

Weitere Links:

• Übungen: Vierecke
• Zur Mathematik Übersicht