Mit den Binomischen Gleichungen befassen wir uns in diesem Artikel. Dabei wird erklärt, was man unter den Binomischen Gleichungen zu verstehen hat und wie man sie anwendet. In diesem Zusammenhang gehen wir auch auf die Binomischen Gleichungen mit höheren Exponenten ein sowie das Ausklammern/Faktorisieren. Dieser Artikel gehört zu unserem Bereich Mathematik.
Wer sich mit der Rechnung rund um Klammern auskennt, der braucht die Binomischen Gleichungen - oder auch Binomische Formeln - eigentlich gar nicht. Denn diese ergeben sich zwangsläufig aus den Rechengesetzen. Warum diese dennoch in der Schule behandelt werden, hat einen einfachen Grund: Sie erleichtern das Leben. Diese drei Gleichungen stellen somit eine "Abkürzung" dar. Und welcher Schüler geht nicht gerne den Weg des geringsten Widerstandes? Bevor wir mit dem Thema richtig loslegen, solltet ihr jedoch die Grundlagen der Klammerrechnung beherrschen. Wer hier noch zweifelt, schaut am Besten schnell einmal in die folgenden Artikel rein. Alle anderen können gleich mit der ersten Binomischen Gleichung loslegen.
Erste Binomische Gleichung
Für alle, die Klammern ausmultiplizieren können, ist die erste binomische Gleichung eigentlich nichts neues, auch wenn sie auf den ersten Blick abschreckend wirkt. Denn diese lautet:
- 1. Binomische Gleichung: (a + b)2 = a2 + 2ab + b2
- Herleitung: (a + b)2 = (a + b) · (a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
Die Herleitung ist für alle diejenigen interessant, die sich Fragen: "Woher kommt das eigentlich?" Alle anderen benötigen nur den mathematischen Ausdruck, den ich fett markiert habe. Die Herleitung zeigt einfach nur, wie man die Klammern ausmultipliziert (was wir im oben verlinkten Abschnitt bereits erklärt haben). Ein paar Beispiele demonstrieren, wie man die Gleichung anwendet:
- (3 + 4)2 = 32 + 2 · 3 · 4 + 42 = 9 + 24 + 16 = 49
- (1 + 2)2 =12 + 2 · 1 · 2 + 22 =1 + 4 + 4 = 9
Tipp: Schaut in die Binomische Gleichung und macht euch klar, was a und b ist. Und dann setzt ihr für a und b die Zahlen ein. Vergleicht die Gleichung mit dem was ich oben vorgerechnet habe, dann sollte es klarer werden. Unsere Übungsaufgaben (Link am unteren Ende des Artikels) dazu sollten ebenfalls für zusätzliche Erleuchtung sorgen.
Zweite Binomische Gleichung
Die zweite binomische Gleichung sieht sehr ähnlich aus. Nur hier findet sich nun ein negatives Vorzeichen. Es folgt wieder die Formel samt Herleitung:
- 2. Binomische Gleichung: (a - b)2 = a2 - 2ab + b2
- Herleitung: (a - b)2 = (a - b) · (a - b) = a2 - ab -ba + b2 = a2 - 2ab + b2
Auch hier geht es letzten Endes darum, in der Aufgabestellung zu sehen "Ok, da ist eine Differenz in der Klammer" und dann einzusetzen. Zum besseren Verständnis auch hier wieder zwei kleine Beispiele:
- (4 - 2)2 = 42 -2 · 4 · 2 + (-2)2 =16 - 16 + 4 = 4
- (3 - a)2 = 32 - 2 · 3 · a + a2 = 9 - 6a + a2
Auch hier wieder der Rat: Vergleicht die 2. Binomische Gleichung von oben mit dem was in den Beispielen gerechnet wurde. Anschließend solltet ihr die Übungsaufgaben machen, welche am unteren Ende des Artikels verlinkt sind.
Dritte Binomische Gleichung
Fehlt uns noch Gleichung Nummer 3. Diese hilft zwei Klammern zu multiplizieren, die wie folgt aussehen:
- 3.Binomische Gleichung: (a + b) (a - b) = a2 - b2
- Herleitung: (a + b) (a - b) = a2 -ab + ba -b2 = a2 - b2
Diese Formel ist somit anzuwenden, wenn man zwei Klammern hat, bei der sich die zweite Variable nur im Vorzeichen anders verhält. Auch hier helfen (hoffentlich) einige Beispiele zur Verdeutlichung:
- (a + 3) (a - 3) = a2 -32 = a2 - 9
- (2 + b) (2 - b) = 22 - b2 = 4 - b2
Spricht man von den Binomischen Gleichungen so denken die meisten an die drei "normalen" Binomischen Gleichungen mit der Hochzahl 2. Hier sehen wir uns nun andere Hochzahlen an. Es geht somit um die Binomische Formeln Hoch 3, 4, 5 etc.
Binomische Gleichungen Hoch 3
Beginnen wir mit den Binomischen Gleichungen wenn der Exponent 3 ist. Zunächst gibt es den kompletten mathematischen Zusammenhang. Danach geht es an die Herleitung und dann sehen wir uns Beispiele an.
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
Herleitung:
Zunächst schreiben wir das Ganze ausführlich hin. Dann multiplizieren wir (a + b) · (a + b) aus und erhalten a2 + 2ab + b2. So wie wir das von den "normalen" Binomischen Gleichung schon kenne. Und dieses Ergebnis multiplizieren wir dann mit (a + b). Es folgen die einzelnen Schritte:
- (a + b)3 = (a + b) · (a + b) · (a + b)
- (a + b)3 = (a + b) · (a2 + ab + ba + b2)
- (a + b)3 = (a + b) · (a2 + 2ab + b2 )
- (a + b)3 = a · a2 + a · 2ab + a · b2 + b · a2 + b · 2ab + b · b2
- (a + b)3 = a3 + 3ab2 + 3a2b + b3
Beispiel :
- (3 + 5)3 = ?
- (3 + 5)3 =33 + 3 · 3 · 52 + 3 · 32 · 5 + 53
- (3 + 5)3 = 512
Weiterer Zusammenhang:
- (a - b)3 = a3 - 3a2b + 3ab2 - b3
Binomische Gleichungen Hoch 4 und 5
Sehen wir uns als nächstes die Ausmultiplikationen für die Potenzen 4 und 5 der Binomischen Gleichung an.
- (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
- (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b 5
- (a - b)4 = a4 - 4a3b + 6a2b2 -4ab3 + b4
- (a - b)5 = a5 - 5a4b + 10a3b2 -10a2b3 +5ab4 -b5
Beispiele für Herleitungen:
Bei den Herleitungen nutzte ich die Ergebnisse für die Potenz 3 um die Potenz 4 zu berechnen. Und im Anschluss verwenden wir dieses Ergebnis wieder um die Potenz 5 zu berechnen. Auf diese Art und Weise kann man auch noch höhere Potenten sowie Differenzen herleiten.
- (a + b)4 = (a + b) · (a3 + 3ab2 + 3a2b + b3)
- (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
- (a + b)5 = (a + b) · ( a4 + 4a3b + 6a2b2 + 4ab3 + b4)
- (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b 5
Beispiel:
- (2 + 3)4 = 24 + 4 · 23 · 3 + 6 · 22 · 32 + 4 · 2 · 33 + 34
- (2 + 3)4 = 625
In diesem Abschnitt geht es nun darum, dass ihr zum Beispiel auf einen Ausdruck wie 4x2 + 12x + 9 die Binomischen Gleichungen rückwärts anwendet. Dabei entsteht ein Ausdruck mit Klammern. Ich zeige gleich Beispiele für alle 3 Binomischen Formeln und wie man dies auf einfache Art und Weise umsetzt. Eines sollte jedoch gleich klar sein: Nicht immer kann man einen solchen Ausdruck so umformen, dass man eine der drei bekannten Binomischen Gleichungen auch anwenden kann. Eine kleine Warnung: Ich stelle hier einen einfachen und praktischen Weg vor um die Aufgaben zu lösen, 100% "schöne" Mathematik wird hier daher nicht gezeigt.
1. Binomische Gleichung Faktorisieren
Eine kurze Erinnerung zur ersten Binomischen Gleichung. Hier lautet der mathematische Zusammenhang (a + b)2 = a2 + 2ab + b2. Und genau diese Gleichung werden wir nun anwenden, um eine Faktorisierung bzw. ein Ausklammern durchzuführen. Zum besseren Verständnis gleich anhand von Beispielen.
Beispiel 1:
Im ersten Beispiel soll 4x2 + 12x + 9 auf die Form (a + b)2 gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a2 = 4x2 und b2 = 9 und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 12x und setzen für a und b noch entsprechend ein. Da die Kontrolle stimmt, ist das Ergebnis richtig und wir können die Lösung notieren. Das sieht also dann so aus:
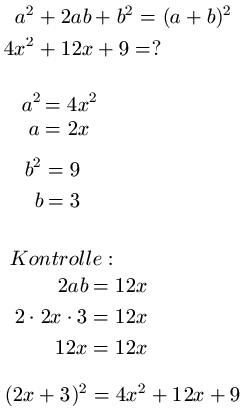
Beispiel 2:
Im zweiten Beispiel soll 9x2 + 12xy + 4y2 auf die Form (a + b)2 gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a2 = 9x2 und b2 = 4y2 und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 12xy und setzen für a und b noch ein. Da die Kontrolle stimmt, ist das Ergebnis richtig und wir können die Lösung notieren. Das sieht also dann so aus:
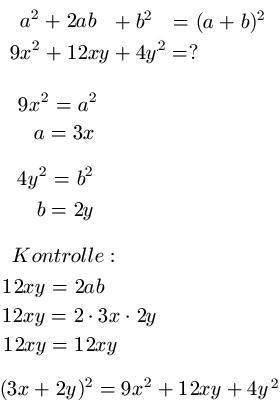
Beispiel 3:
Im dritten Beispiel soll 9x2 + 14xy + 4y2 auf die Form (a + b)2 gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a2 = 9x2 und b2 = 4y2 und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 14xy und setzen für a und b noch ein. Da die Kontrolle nicht stimmt, ist das Ergebnis falsch!! Die erste Binomische Formel kann hier also nicht eingesetzt werden. Das sieht also dann so aus:
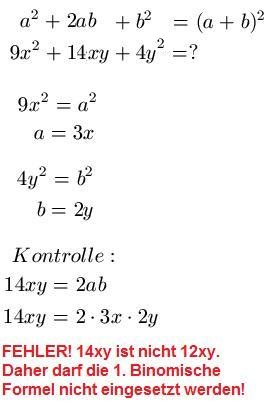
2. Binomische Gleichung Faktorisieren
Kommen wir als nächstes zur Faktorisierung der 2. Binomischen Gleichung. Für diese lautete der mathematische Zusammenhang: (a - b)2 = a2 - 2ab + b2. Und genau auf diese Form bringen wir nun wieder einige Beispiele.
Beispiel 4:
Im vierten Beispiel soll 16x2 - 72xy + 81y2 auf die Form (a - b)2 gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a2 = 16x2 und b2 = 81y2 und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 72xy und setzen für a und b noch ein. Da die Kontrolle stimmt, ist das Ergebnis richtig und wir können die Lösung notieren. Das sieht also dann so aus:
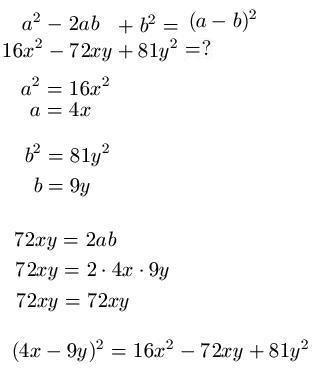
Beispiel 5:
Im fünften Beispiel soll 16x2 - 80xy + 81y2 auf die Form ( a - b )2 gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a2 = 16x2 und b2 = 81y2 und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 80xy und setzen für a und b noch ein. Da die Kontrolle nicht stimmt, ist das Ergebnis falsch und wir können die Lösung verwerfen. Das sieht also dann so aus:

3. Binomische Gleichung Ausklammern
Fehlt uns noch das Ausklammern bzw. Faktorisieren bei der 3. Binomischen Gleichung. Die Vorgehensweise sieht ähnlich aus zu den schon vorgestellten Beispielen. Für die letzte Formel gilt der Zusammenhang: (a + b) (a - b) = a2 - b2. Auch hier sehen wir uns gleich einmal Beispiele an.
Beispiel 6:
Im sechsten Beispiel soll 9x2 - 4y2 auf die Form (a + b)(a - b) gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a2 = 9x2 und b2 = 4y2 und berechnen jeweils das positive Ergebnis für a und b. Das sieht also dann so aus:
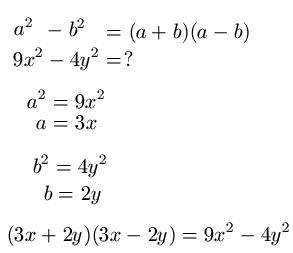
Links:
239 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
