Mit diesem Artikel lernst du die Prozentrechnung. Du erfährst was Prozent bedeutet und was es mit Grundwert, Prozentwert und Prozentsatz auf sich hat. Mit Beispielen zur Prozentrechnung lernst du die Formeln anzuwenden. Am Ende vom Artikel geht es um die Anwendung der Prozentrechnung beim Dreisatz und der Zinsrechnung.
Um die Prozentrechnung zu verstehen, musst du wissen, was Prozent bedeutet. Prozent bedeutet nichts anderes als Hundertstel. Ein Prozent ist daher nicht anderes als der hundertste Teil. Das Zeichen für Prozent ist das Prozentzeichen (%).
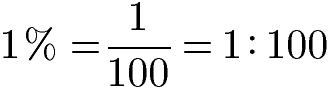
Beispiel: 5 Prozent
Die Angabe 5 % (gesprochen: Fünf Prozent) bedeutet 5 von 100 Teile. Dies kann auch in Form eines Bruchs oder einer Division dargestellt werden.
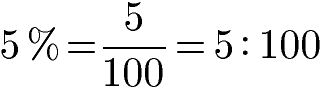
Prozentangaben können optisch dargestellt werden. Sind 5 von 100 Felder grün sind dies 5 Prozent der Felder.

Sehen wir uns nun eine sehr einfache Erklärung zur Prozentrechnung an sowie wichtige Formeln.
Prozentrechnung für Dumme einfach erklärt
Oftmals wünschen sich viele Schüler und Schülerinnen eine einfache Erklärung der Prozentrechnung für Dumme. Daher versuche ich nun eine möglichst einfache Erklärung des Prozentrechnens. In der Prozentrechnung gibt es drei wichtige Begriffe: Grundwert, Prozentsatz und Prozentwert.
Beispiel 1: Prozentrechnung Erklärung
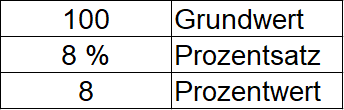
Als Beispiel haben wir 100 Felder. Es sollen 8 % (gesprochen: 8 Prozent) blau angemalt werden. Dies bedeutet, dass 8 Felder blau angemalt werden. Der Grundwert ist damit 100, der Prozentsatz 8 % und der Prozentwert 8.
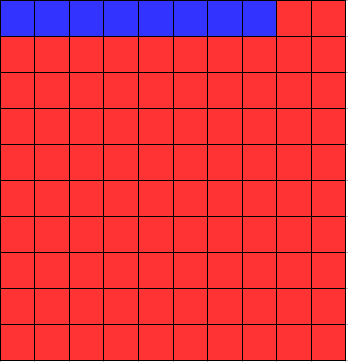
Optisch dargestellt bedeutet dies, dass 8 von 100 Felder blau angemalt werden.
Beispiel 2: Prozentrechnung Erklärung
Nicht immer bezieht sich der Prozentsatz auf 100 Teile. Im nächsten Beispiel gibt es insgesamt 200 Teile, daher ist der Grundwert 200. Es sollen ebenfalls 8 % blau angemalt werden. Die Angabe 8 % bedeutet 8 von 100 Teilen oder eben 16 von 200 Teilen.
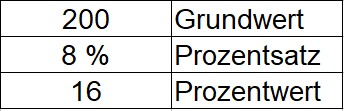
Grafisch kann dies mit 200 Feldern dargestellt werden, von denen 16 blau sind.

Wie können Grundwert, Prozentsatz und Prozentwert berechnet werden? Sehen wir uns dazu Formeln der Prozentrechnung und Beispiele an.
Prozentrechnung Formeln und Dreieck
In der Prozentrechnung werden Formeln verwendet um Grundwert, Prozentwert und Prozentsatz (Prozentzahl) zu berechnen. In den Formeln werden für die Begriffe Abkürzungen verwendet. Der Grundwert wird mit G abgekürzt, W ist der Prozentwert, p die Prozentzahl und der Prozentsatz wird mit p % angegeben.
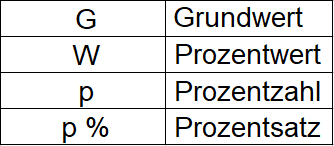
Hinweis: In der Prozentrechnung wird zwischen Prozentzahl und Prozentsatz unterschieden. Dabei ist der Prozentsatz die Angabe mit Prozentzeichen und die Prozentzahl ohne Prozentzeichen. Der Prozentsatz p % = 40 % entspricht der Prozentzahl p = 40.
Die Formeln der Prozentrechnung können sowohl mit Gleichungen als auch mit Dreiecken dargestellt werden. Sehen wir uns die entsprechenden Gleichungen und Dreiecke einmal an, unterhalb gibt es Beispiele mit Zahlen und Einheiten.
Grundwert berechnen:
Der Grundwert wird berechnet, indem der Prozentwert mit 100 multipliziert wird. Außerdem muss durch die Prozentzahl geteilt werden. Die Formel kann sowohl in Form einer Gleichung als auch mit einem Dreieck dargestellt werden.
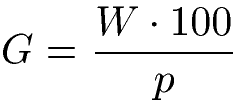
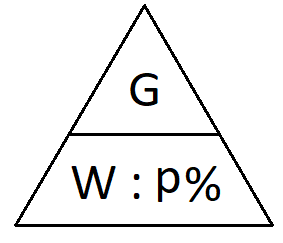
Prozentwert berechnen:
Der Prozentwert wird berechnet, indem die Prozentzahl mit dem Grundwert multipliziert und durch 100 geteilt wird. Die Formel kann sowohl in Form einer Gleichung als auch mit einem Dreieck dargestellt werden.
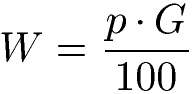
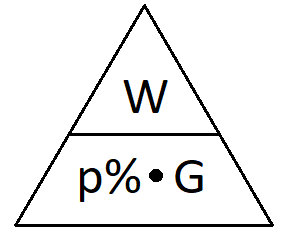
Prozentsatz (Prozentzahl) berechnen:
Der Prozentsatz entspricht der Prozentzahl geteilt durch 100. Beispiel: Der Prozentsatz p % = 21 entspricht der Prozentzahl p = 21. Diesen Zusammenhang zwischen Prozentsatz und Prozentzahl findest du auch in der nächsten Gleichung.
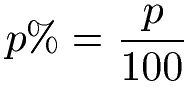
Die Prozentzahl wird berechnet, indem der Prozentwert mit 100 multipliziert und durch den Grundwert geteilt wird. Die Formel kann sowohl in Form einer Gleichung als auch mit einem Dreieck dargestellt werden.
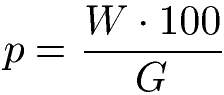
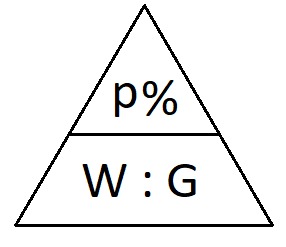
Wie werden die Formeln zur Prozentrechnung verwendet? Sehen wir uns zu den Formeln einige Beispiele an.
Prozentrechnen: Prozentwert berechnen
In der Prozentrechnung gibt der Prozentwert den zahlenmäßigen Anteil vom Ganzen an. Um den Prozentwert zu berechnen wird die Prozentzahl mit dem Grundwert multipliziert und durch 100 geteilt.
Prozentwert Beispiel 1:
In einen Jahrgang gehen 180 Schüler. Davon kommen 25 % der Schüler zu Fuß in die Schule. Wie viele Schüler kommen zu Fuß in die Schule?
Lösung: Gesucht ist ein Teil der Schüler, also der Prozentwert. Gegeben ist die Gesamtzahl der Schüler, der Grundwert ist G = 180. Der Prozentsatz ist p % = 25 %, daher ist die Prozentzahl p = 25. Diese Angaben setzen wir in die Formel ein.
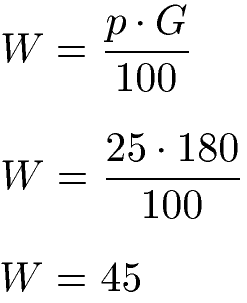
Von den 180 Schüler kommen 45 Schüler zu Fuß.
Prozentwert Beispiel 2:
Ein Tisch kostet 140 Euro. Er wird jedoch aktuell mit 20 Prozent Rabatt verkauft. Was kostet der Tisch noch?
Lösung: Der ursprüngliche Preis ist der Grundwert G mit 140 Euro. Gesucht ist der Anteil des Geldes nach dem Rabatt. Der Rabatt beträgt 20 Prozent, der Tisch kostet damit nicht mehr den vollen Preis (100 %), sondern 20 % weniger, daher noch 80 % des alten Preises. Wir setzen daher die Prozentzahl p = 80 in die Formel ein.
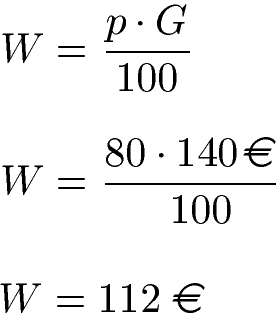
Ein Rabatt von 20 Prozent bedeutet der Tisch kostet nicht mehr 140 Euro, sondern 112 Euro.
Prozentrechnen: Grundwert ausrechnen
In der Prozentrechnung ist der Grundwert "das Ganze" auf welche sich die Rechnung bezieht. Der Grundwert lässt sich berechnen, in dem der Prozentwert mit 100 multipliziert und durch die Prozentzahl geteilt wird.
Grundwert Beispiel 1:
45 Schüler eines Jahrgangs kommen morgens zu Fuß in die Schule. Dies sind 25 Prozent der Schüler. Wie viele Schüler gehen in den Jahrgang?
Lösung: Der Anteil der Schüler welche zu Fuß in die Schule kommen ist der Prozentwert, daher W = 45. Der Prozentsatz ist p % = 25 % oder als Prozentzahl p = 25. Wir setzen dies in die Formel ein.
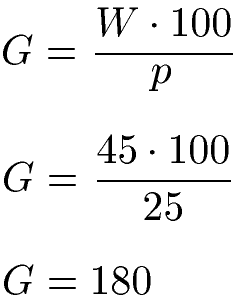
Insgesamt gehen 180 Schüler in diesen Jahrgang.
Grundwert Beispiel 2:
Ein Tisch wurde auf 80 Prozent seinen ursprünglichen Preises reduziert. Jetzt kostet der Tisch noch 112 Euro. Was kostete dieser vorher?
Lösung: Der Anteil am ursprünglichen Preis liegt noch bei 112 Euro, daher W = 112 Euro. Gesucht ist der frühere Preis, also der Grundwert. Der Prozentsatz ist p % = 80 % und damit die Prozentzahl p = 80.
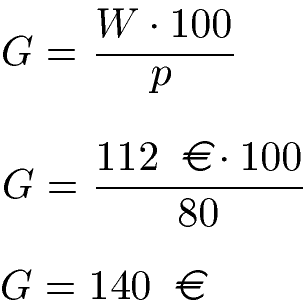
Bevor der Rabatt gewährt wurde kostete der Tisch 150 Euro.
Prozentrechnen: Prozentsatz und Prozentzahl
Der Prozentsatz gibt den Anteil am Ganzen an. Im Internet und in Formelsammlungen werden oft Prozentsatz und Prozentzahl vermischt. Die Prozentzahl ist dabei eine Angabe ohne Prozentzeichen, der Prozentsatz eine Angabe mit Prozentzeichen.
Prozentsatz Beispiel 1:
In einem Jahrgang kommen 45 der 180 Schüler zu Fuß in die Schule. Wie viel Prozent der Schüler sind dies?
Lösung: Insgesamt sind es 180 Schüler, daher G = 180. Der Anteil der Schüler zu Fuß sind 45 Schüler, daher W = 45. Wir setzen dies in die Gleichung ein und rechnen den Prozentsatz aus.
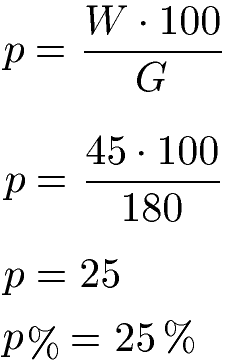
Die Prozentzahl ist p = 25. Daher ist der Prozentsatz p % = 25 %.
Prozentsatz Beispiel 2:
Ein Tisch wurde von 140 Euro auf 112 Euro Kaufpreis reduziert. Wie groß ist der Preisnachlass in Prozent?
Lösung: Wir setzen den Grundwert G = 140 Euro und Prozentwert W = 112 Euro in die Gleichung ein.
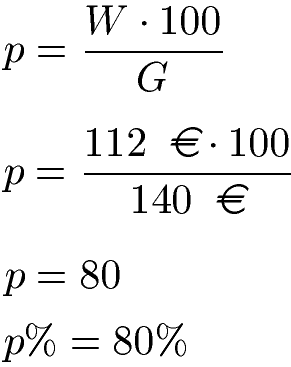
Wir erhalten eine Prozentzahl von p = 80 und damit einen Prozentsatz von p % = 80 %.
Anwendung Prozentrechnung: Dreisatz
Eine Anwendung der Prozentrechnung ist der Dreisatz. Beim Dreisatz geht es darum eine Angabe erst auf 1 Stück bzw. 1 Prozent runter zu rechnen um dann auf das Ziel wieder hochzurechnen.
Beispiel 1: Prozentrechnung durch Dreisatz
In einen Jahrgang gehen 180 Schüler. 25 Prozent davon kommen zu Fuß in die Schule. Wie viele Schüler sind dies?
Lösung: 180 Schüler sind alle Schüler im Jahrgang, daher 100 Prozent. Wir rechnen zunächst auf 1 Prozent runter, müssen daher die 100 % durch 100 teilen und auch die Schülerzahl von 180 wird durch 100 geteilt. Gesucht sind jedoch 25 Prozent, daher muss noch einmal mit 25 multipliziert werden. Damit sind 45 Schüler zu Fuß unterwegs.
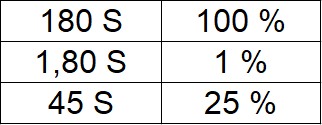
Beispiel 2: Prozentrechnung durch Dreisatz
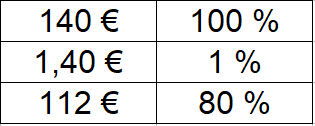
Ein Tisch kostet 140 Euro. Der Preis wird um 20 Prozent gesenkt, sprich der Tisch kostet nach dem Rabatt noch 80 Prozent des vorigen Preises. Wie teuer ist der Tisch?
Lösung: 140 Euro sind der gesamte Preis, den der Tisch einmal gekostet hat. Dies sind 100 Prozent des Preises. Wir teilen zunächst durch 100 um 1 Prozent auszurechnen und damit 1,40 Euro. Gesucht sind 80 Prozent des Preises, daher wird mit 80 multipliziert. Der Tisch kostet nach dem Rabatt noch 112 Euro.
Anwendung Prozentrechnung: Zinsrechnung
Eine Anwendung der Prozentrechnung ist die Zinsrechnung. In der Zinsrechnung geht es um das Rechnen mit Geld. Die Begriffe und Variablen in den Formeln ändern sich dabei ein wenig:
- Der Grundwert wird zum Kapital.
- Der Prozentsatz wird zum Zinssatz.
- Der Prozentwert wird zu den den Zinsen.
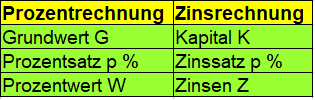
Die Formeln der Zinsrechnungen dienen dazu die Zinsen (Z), das Kapital (K) und den Zinssatz bzw. die Zinszahl (p) zu berechnen.
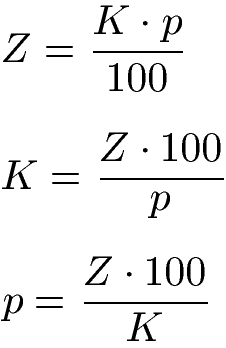
Beispiel Zinsrechnung:
Ein Betrag von 3500 Euro wird für ein Jahr zu einem Zinssatz von 4 Prozent angelegt. Wie hoch sind die Zinsen? Zur Lösung setzen wir das Kapital und die Zinszahl in die Gleichung ein und berechnen 140 Euro Zinsen.
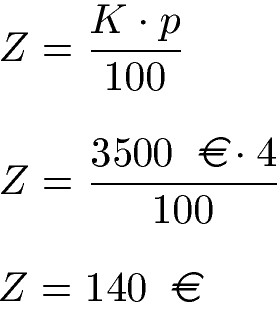
Links:
- Prozentrechnung Aufgaben mit Lösungen
- Grundwert berechnen
- Prozentwert berechnen
- Prozentsatz berechnen
- Dreisatz
- Zinsrechnung
- Mathematik-Übersicht
484 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: