Einheitskreis

Mit dem Einheitskreis befassen wir uns in diesem Artikel. Dabei zeige ich euch zunächst was man unter einem Einheitskreis versteht und gehe dann auf trigonometrische Funktionen sowie Schwingungen ein. Außerdem wird die Umrechnung Bogenmaß zu Gradmaß erklärt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Beginnen wir mit etwas ganz einfachem: Was ist ein Einheitskreis? Darunter versteht man einen Kreis mit dem Radius von 1. Manchmal zeichnet man sich noch ein Koordinatensystem ein. Der Ursprung dieses Koordinatensystems fällt mit dem Mittelpunkt des Kreises zusammen. Ein Einheitskreis sieht so aus:

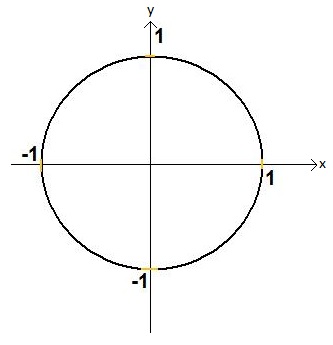
Einheitskreis und trigonometrische Funktionen

Jeder erinnert sich hoffentlich noch an den Satz des Pythagoras und an die Definitionen Ankathete, Gegenkathete und Hypotenuse. Falls nicht, hier noch einmal eine kurze Gedächtnishilfe. Also wir haben ein Dreieck mit einem rechten Winkel. Dann haben wir den Winkel Alpha. Die Seite am Winkel heißt Ankathete, die Seite gegenüber des Winkels Gegenkathete. Die längste Seite wird Hypotenuse genannt.

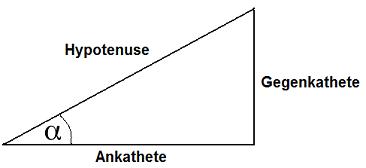
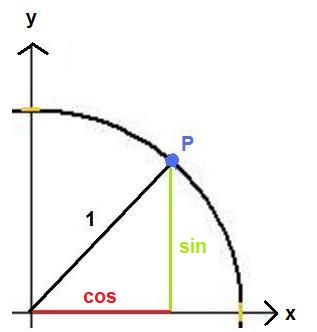
Und das Zeichnen wir nun zu der Grafik des Einheitskreises hinzu, also haben wir den Einheitskreis sowie ein rechtwinkliges Dreieck mit Ankathete, Gegenkathete und Hyptonuse. Ich stelle dabei nur ein Viertel des Kreises da, damit man auf der Grafik noch etwas erkennen kann.

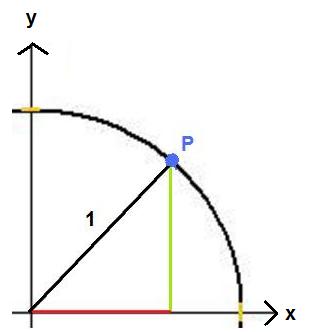
Wir haben damit eine Hypotenuse mit der Länge 1 in schwarz gezeichnet, die Gegenkathete in grün und die Ankathete in rot. Außerdem noch ein Punkt P in blau, der auf dem Kreis liegt. Mit diesem Wissen definieren wir nun die Sinusfunktion, die Kosinusfunktion und im Anschluss auch den Tangens.

Sinus am Einheitskreis:

Ist P der zum Winkel Alpha gehörende Punkt auf dem Einheitskreis, so gilt per Definition für den Sinus von Alpha die Beziehung:

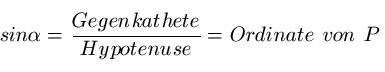
Ordinate? Was war das doch gleich? Das ist die "Höhe" sozusagen. Also der Abstand von der roten Linie bis zum Punkt.

Kosinus am Einheitskreis:

Den Kosinus des Winkels Alpha findet man als Abszissenwert des Punktes P beim Einheitskreis. Mit dem Wissen, dass die Hypotenuse = 1 ist, erhalten wir damit:

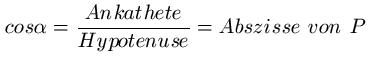
Tangens:

Den Tangens erhält man, in dem man den Sinus durch den Kosinus dividiert:

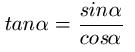
Einheitskreis und Schwingungen

So noch einmal die Grafik von vorhin, diesmal jedoch mit sinus in grün und cosinus in rot. Denn genau das brauchen wir nun für Schwingungen:

Einheitskreis und Sinus-Schwingung:

Stellt euch folgendes vor:

1. Ein Pfeil zeigt zunächst vom Mittelpunkt des Kreises nach rechts, der Punkt P liegt also auf der X-Achse.
2. Damit hat  die "grüne Linie" die Länge von Null.
3. Nun bewegt sich der Punkt auf dem Kreis nach oben, dann nach links, nach unten und dann nach rechts.  Dabei wird die grüne Linie zunächst länger, bis sie auf +1 bei der Y-Achse steht, danach wird sie wieder kürzer bis sie durch die X-Achse hindurchtritt und der Wert negativ wird bis hin zur -1. Und schließlich wird wieder die Ausgangslage erreicht.
4. Und zeichnet man das auf, erhält man eine Sinus-Schwingung:

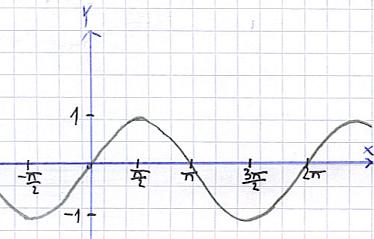
Einheitskreis und Kosinus-Schwingung:

Das Ganze machen wir nun noch mit der roten Linie. Diese ist, wenn der Pfeil nach rechts zeigt zunächst bei der Länge 1. Daher beginnt die Kosinus-Schwingung bei +1. Bewegt sich der Punkt P auf dem Einheitskreis nun gegen den Uhrzeigersinn, so wird die rote Linie zunächst kürzer, anschließend wird sie negativ bis die -1 erreicht wird und danach wird sie wieder positiv bis zu +1. Dadurch erhält man eine Kosinus-Schwingung, die wie folgt aussieht:

Gradmaß und Bogenmaß

Manchmal benötigt man Angaben im Gradmaß und manchmal im Bogenmaß. Wann man dies jeweils benötigt und wie man die Angaben ineinander umrechnen kann, das soll nun in diesem Abschnitt gezeigt werden.

Das Gradmaß:

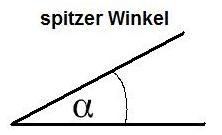
In der Schule lernt man normalerweise zunächst das Gradmaß kennen. Dabei entspricht eine komplette Umrundung eines Kreises 360 Grad. Steht also eine Person in einem Raum und dreht sich einmal um sich herum, so dass sie wieder in die gleiche Richtung blickt wie vor der Drehung, dann wurden dabei 360 Grad überschritten.  Ein weiteres Beispiel: Wir haben zwei Geraden und zwischen diesen bildet sich ein Winkel aus. Dieser wird in der folgenden Grafik als α ( gesprochen Alpha ) bezeichnet und ist so in etwa 40 Grad.

Das Bogenmaß:

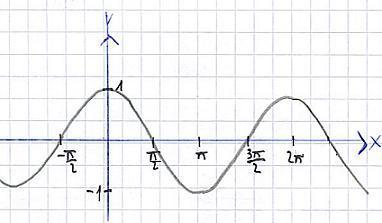
In der Mathematik, vor allem aber auch in der Physik ist das Bogenmaß von Interesse. Ein oft verwendetes Beispiel dafür ist eine Schwingung, zum Beispiel der Sinus. Wird ein Sinusverlauf komplett vollzogen, so hat man ebenfalls 360 Grad durchlaufen, oder im Bogenmaß ausgedrückt 2π. Die folgende Grafik zeigt den Verlauf eines Sinus.

Bogenmaß und Gradmaß umrechnen / umwandeln

Wie im letzten Abschnitt bereits angedeutet, entsprechen 360 Grad im Gradmaß 2π im Bogenmaß. Damit haben wir eigentlich schon eine Möglichkeit gefunden, diese beiden Angaben ineinander umzurechnen. Die Formeln dafür lauten:

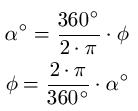
Beispiele:

Das Gradmaß 23° soll ins Bogenmaß umgerechnet werden.

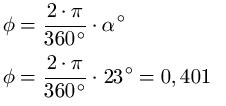
Das Bogenmaß 0,6 rad soll ins Gradmaß umgewandelt werden.

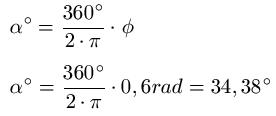
Links:

• Zur Mathematik-Übersicht