Mit der "Ableitung von x" - sprich dem Ableiten von Funktionen - befassen wir uns in diesem Artikel. Dabei erklären wir euch, wie man so eine Ableitung durchführt und welche Regeln man dafür einsetzt. Dieser Artikel gehört zum Bereich Mathematik.
Wie leitet man eine Funktion ab, die von "x" abhängt? In der Mathematik gibt es verschiedene Regeln um eine Funktion abzuleiten. In diesem Artikel stellen wir euch diese Ableitungsregeln vor. Für eine ausführliche Darstellung ( Beispiele + Videos ) werden weitere Informationen verlinkt. Zum besseren Verständnis werden auch schon einige Beispiele gezeigt.
Ableitung x: Faktorregel / Potenzregel
Starten wir mit der Faktorregel und Potenzregel. Ziel ist es, Funktionen wie zum Beispiel x4 oder 3x2 oder auch 5x abzuleiten. Allgemein gilt: y = xn mit der Ableitung y' = n · xn-1. Hier die allgemeine Anwendung, einige Beispiele folgen im Anschluss:
- Schreibt euch die Funktion y = ... auf
- Schreibt darunter y' =
- Schreibt den Exponent von y hinter y' =
- Schreibt dann das x hin
- Der Exponent für die Ableitung wird um eins reduziert.
- Ein Faktor bleibt erhalten.
Beispiel: y(x) = x2 , y'(x) = 2x
Summenregel ( Ableitung x )
Die Summenregel besagt: Bei einer endlichen Summe von Funktionen darf gliedweise differenziert werden. Auch dies lässt sich am Besten anhand von einigen Beispielen zeigen. Dabei wird eine Ableitung in Bezug auf x vorgenommen.
Beispiele:
Tabelle nach rechts scrollbar|
y = f(x) |
y' = f'(x) |
| x2 + x2 |
2x + 2x |
| 3x + 2x3 | 3 + 2 · 3 · x2 |
| 5x2 + 10x3 |
5 · 2x + 10 · 3x2 |
| 3x2 + 2x3 + 4x3 |
3 · 2x + 2 · 3x2 + 4 · 3x2 |
Ableitungsregel: Produktregel
Kommen wir zur Produktregel. Diese wird eingesetzt, wenn eine Funktion in Produktform vorliegt. Es folgt zunächst einmal die Formel dieser Ableitungsregel. Danach folgen Erklärungen und Beispiele, wobei die Ableitung nach x durchgeführt wird.
Produktregel: Kurzschreibweise
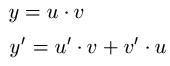
Ihr müsst bei der Funktion einen Teil als u und einen Teil als v bezeichnen. Diesen jeweiligen Teil leitet ihr ab und setzt diese in die Gleichung von y' ein. Die folgenden Beispiele zeigen euch dies:
Beispiel 1:
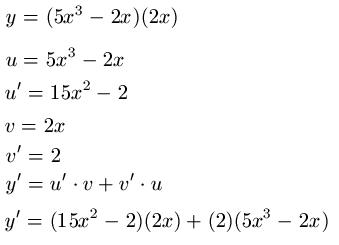
Quotientenregel ( Ableitung von x )
Nach der Produktregel, kommen wir nun zur Quotientenregel. Auch bei dieser wird eine Ableitung in Bezug auf x durchgeführt. Diese kommt zum Einsatz, wenn ihr einen Bruch ableiten wollt. Wie immer zunächst die allgemeine Regel, danach einige Erklärungen und Beispiele.
Quotientenregel: Kurzschreibweise
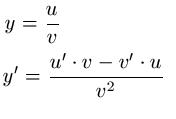
Den Zähler setzt ihr u, den Nenner setzt ihr v. Leitet diese dann beide ab und setzt dies in y' ein. Das folgende Beispiel verdeutlicht dies:
Beispiel 1:
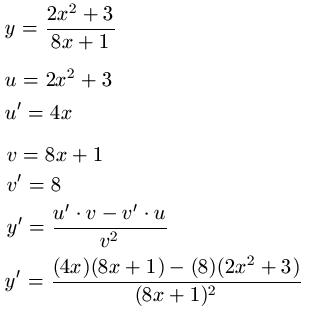
Kettenregel einsetzen, Ableitung x
Mit den bisherigen Ableitungsregeln ist es möglich, einfache Funktionen abzuleiten. Problematisch wird es jedoch, wenn zusammengesetzte oder gar verschachtelte Funktionen abgeleitet werden müssen. Um Funktionen wie zum Beispiel y = sin ( 5x - 8 ) oder y = e4x abzuleiten, muss die Kettenregel eingesetzt werden. Man greift dabei auf eine so genannte Substitution zurück. Was genau es damit auf sich hat, erkläre ich euch noch. Zunächst jedoch ein kleiner Merksatz.
Kettenregel: Die Ableitung einer zusammengesetzten ( verketteten ) Funktion erhält man als Produkt aus äußerer und innerer Ableitung.
Viele Schüler haben zu Beginn größere Schwierigkeiten diese Regel anzuwenden. Grund: Es gehört etwas Erfahrung dazu, um zu sehen, dass die Kettenregel überhaupt angewendet werden muss. Im nun Folgenden stelle ich euch einige typische Beispiele vor, bei der durch Anwendung der Kettenregel die Ableitung gebildet wird. Dabei wird zunächst der Rechenweg gezeigt, darunter finden sich Erläuterungen. Auch hier wird eine Ableitung in Bezug auf x vorgenommen.
Beispiel 1: y = ( 3x - 2 )8
- Substitution: u = 3x - 2
- Äußere Funktion = u8
- Äußere Ableitung = 8u7
- Innere Funktion = 3x -2
- Innere Ableitung = 3
- y' = 8u7 · 3 = 24u7
- mit u = 3x - 2 => y' = 24 ( 3x - 2 )7
Links:
459 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: