Assoziativgesetz einfach erklärt ▷ mit Beispielen

Das Assoziativgesetz für die Addition, Subtraktion, Multiplikation und Division wird hier erklärt. Ihr lernt dabei in welchen Fällen das Assoziativgesetz eingesetzt werden darf und welche Fehler ihr nicht machen dürft. Dieser Artikel gehört zum Bereich Mathematik.

Was ist das Assoziativgesetz? Zunächst eine Erklärung bzw. Definition zu diesem Rechengesetz

Hinweis:

Das Assoziativgesetz sagt aus, dass bei einer Addition oder Multiplikation drei oder mehr Zahlen vertauscht werden dürfen ohne das sich das Ergebnis der Berechnung ändert. Das Assoziativgesetz wird im Deutschen auch als Verknüpfungsgesetz oder Verbindungsgesetz bezeichnet.

Assoziativgesetz Addition:

In der Mathematik spielt es keine Rolle in welcher Reihenfolge die Zahlen bei einer Addition stehen. Beim Kommutativgesetz wurde bereits geklärt, dass es bei der Addition von zwei Zahlen nicht auf die Reihenfolge ankommt. Das Assoziativgesetz erweitert diese Regel: Auch bei 3 oder mehr Zahlen spielt die Reihenfolge der Zahlen keine Rolle für das Ergebnis (Summe) der Aufgabe. Dieses Rechengesetz lässt sich mit folgender Formel ausdrücken.

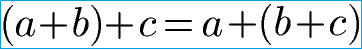
Assoziativgesetz Addition Beispiel:

Das nächste Beispiel zeigt, dass es keine Rolle spielt in welcher Reihenfolge drei Zahlen addiert werden.

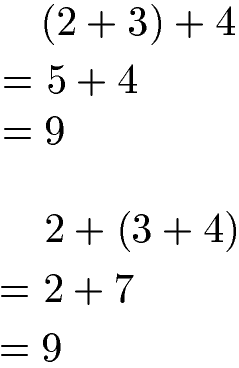
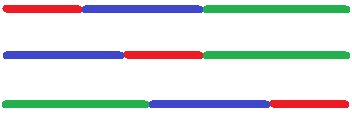
Dies lässt sich auch grafisch mit drei Strecken verdeutlichen. Eine rote, eine blaue und eine grüne Strecke werden in beliebiger Reihenfolge aneinander gehängt. Die gesamte Länge (Summe) ist dabei in allen Fällen gleich.

Assoziativgesetz bei der Subtraktion

Nach der Addition ist die Subtraktion die zweite Grundrechenarten. Merke: Das Assoziativgesetz gilt nicht für die Subtraktion! Die Reihenfolge der Zahlen bei einer Subtraktion ist wichtig. Werden bei einer Subtraktion die Zahlen vertauscht ist das Ergebnis (Differenz) meistens unterschiedlich. Die Ungleichung um dies zu beschreiben lautet:

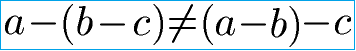
Assoziativgesetz Subtraktion Beispiel:

Zwischen die Zahlen 8, 4 und 2 werden Minuszeichen geschrieben und durch Klammern die Reihenfolge der Berechnung verändert. Da in der Mathematik zunächst immer die Klammer berechnet werden muss entstehen verschiedene Rechenwege mit unterschiedlichen Ergebnissen.

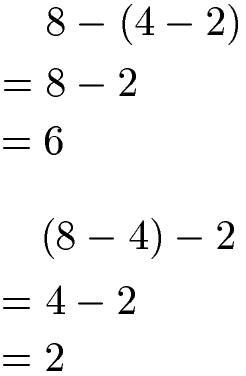
Merke: Bei der Subtraktion dürfen Minuend und Subtrahend nicht vertauscht werden! Für die Subtraktion gilt das Assoziativgesetz nicht.

Assoziativgesetz Multiplikation

Neben der Addition gilt das Assoziativgesetz auch bei der Multiplikation. Es spielt keine Rolle in welche Reihenfolge die Zahlen bei Multiplikationen berechnet werden. Das Ergebnis (Produkt) ist stets gleich. Die Formel zur Multiplikation beim Assoziativgesetz lautet:

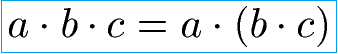
Assoziativgesetz Multiplikation Beispiel 1:

Die Zahlen 2, 3 und 4 werden in verschiedener Reihenfolge miteinander multipliziert. Sofern vorhanden wird eine Klammer zuerst berechnet. Wie man sehen kann spielt die Reihenfolge der Berechnung für das Produkt - in diesem Fall 24 - keine Rolle.

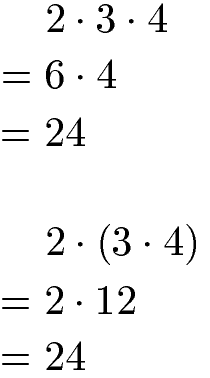
Assoziativgesetz Multiplikation Beispiel 2:

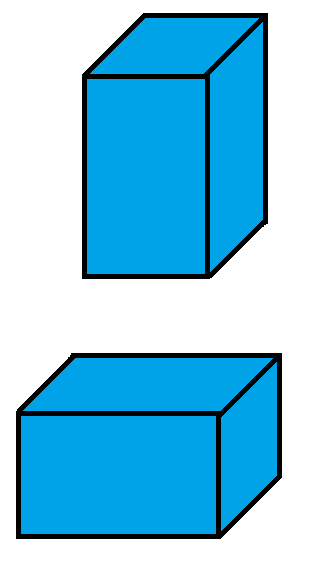
Eine praktische Anwendung für das Assoziativgesetz der Multiplikation ist das Volumen eines Quaders. Die Strecken für Länge, Breite und Höhe können beliebig vertauscht werden. Am Volumen des Körpers ändert sich dadurch nichts. In beiden Fällen sind die Volumen - hier blau eingezeichnet - gleich groß.

Assoziativgesetz für die Division

Das Assoziativgesetz gilt nicht für die Subtraktion und auch nicht für die Division. Die Reihenfolge der Zahlen bei einer Division ist wichtig! Sie darf nicht vertauscht werden. Die Ungleichung um dies zu zeigen lautet:

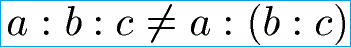
Assoziativgesetz Division Beispiel 1:

Die zahlen 20, 10 und 2 werden dividiert. Dabei wird die Reihenfolge der Berechnung durch eine Klammer verändert. Wie das Beispiel zeigt entsteht durch die unterschiedliche Reihenfolge der Berechnung ein anderer Quotient.

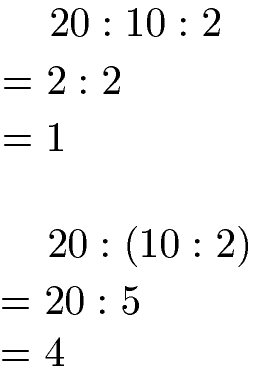
Weitere wichtige Rechenregeln sind das Kommutativgesetz und das Distributivgesetz.

Links:

• Assoziativgesetz Aufgaben / Übungen
• Zur Mathematik-Übersicht