Geometrie: Volumen und Oberfläche von Quader, Zylinder und Kugel

In diesem Abschnitt beschäftigen wir uns mit dem Volumen und Oberflächen von räumlichen Körpern. Wir kümmern uns zunächst um drei oft in der Realität vorkommende Körper: Dem Quader, Zylinder und der Kugel.

Eine kleine Warnung vorweg: Wenn ihr mit Volumen und Oberflächen rechnet, müsst ihr immer die gleiche Maßeinheit zum Rechnen nutzen. Also nicht Meter und Millimeter in eine Formel einsetzen, sondern entweder alles erst in Meter umrechnen und dann einsetzen oder alles erst in Millimeter umrechnen und diese dann einsetzen.

Volumen und Oberfläche Video:
Dieser Artikel liegt auch als Video vor.

• Hinweise: Der Abruf ist direkt in der Rubrik Volumen + Oberfläche Video möglich.
• Probleme: Bei Abspielproblemen bitte den Artikel Video Probleme aufrufen.

Quader: Volumen und Oberfläche

Beginnen wir mit dem Quader. Die folgende Grafik zeigt, wie dieser Körper aussieht.

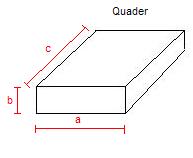
Volumen des Quaders:

Formel:

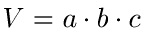
• "V" ist das Volumen des Quaders
• "a" ist die Länge des Quaders
• "b" ist die Breite des Quaders
• "c" ist die Tiefe des Quaders

Beispiel: a = 4 cm, b = 3 cm, c = 2 cm

Lösung:

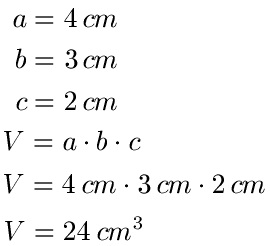
Oberfläche des Quaders:

Formel:

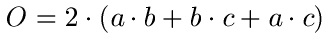
• "O" ist die Oberfläche des Quaders
• "a" ist die Länge des Quaders
• "b" ist die Breite des Quaders
• "c" ist die Tiefe des Quaders

Beispiel: a = 2 cm, b = 4 cm, c = 6 cm

Lösung:

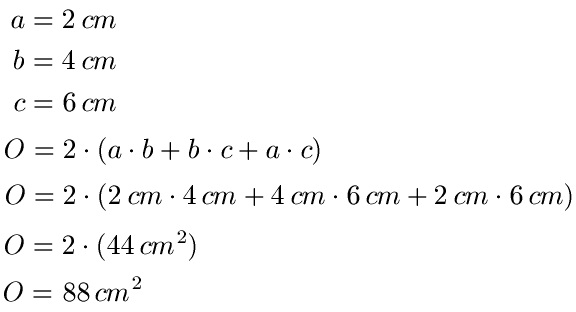
Zylinder: Volumen

Beschäftigen wir uns mit einem Zylinder und dessen Volumen. Doch zunächst auch hier erst einmal eine Grafik.

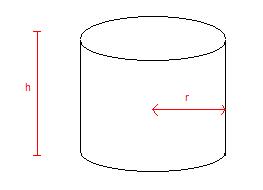
Volumen Zylinder:

Formel:

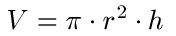
• "V" ist das Volumen des Zylinder
• "π" ist die Kreiszahl ( 3,14159 )
• "r" ist der Radius des Zylinder
• "h" ist die Höhe des Zylinder

Beispiel: r = 5 cm, h = 10 cm

Lösung:

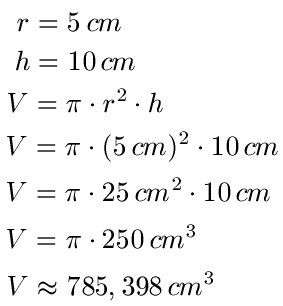
Oberfläche Zylinder:

Formel:

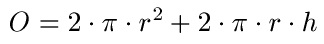
Beispiel: r = 5 cm, h = 8 cm

Lösung:

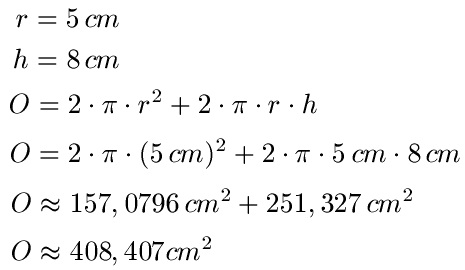
Kugel: Oberfläche und Volumen

Kommen wir nun zur Oberfläche und Volumen einer Kugel. Zunächst erneut eine Grafik:

Volumen einer Kugel

Formel:

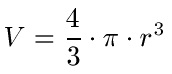
• "V" ist das Volumen der Kugel
• "π" ist die Kreiszahl ( 3,14159 )
• "r" ist der Radius der Kugel

Beispiel: r = 2 cm

Lösung:

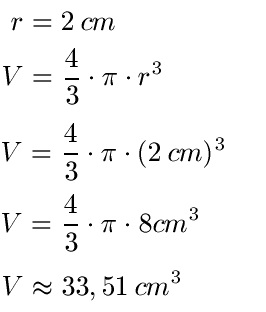
Oberfläche einer Kugel

Formel:

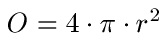
• "O" ist die Oberfläche der Kugel
• "π" ist die Kreiszahl ( 3,14159 )
• "r" ist der Radius der Kugel

Beispiel: r = 2 cm

Lösung:

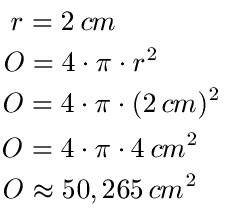
Links:

• Zu den Übungsaufgaben "Volumen und Oberfläche"
• Zum Artikel "Zirkel"
• Zurück zur Geometrie-Übersicht
• Zurück zur Mathematik-Übersicht