In diesem Abschnitt zur Trigonometrie zeigen wir euch, wir ihr mit Sinus, Cosinus / Kosinus und Tangens Winkel berechnen könnt. Dabei lernt ihr Begriffe wie Ankathete, Gegenkathete und Hypotenuse kennen. Neben Erklärungen und Beispielen findet ihr zu dem auch Übungsaufgaben, um mit den Inhalten selbst besser zurecht zu kommen.
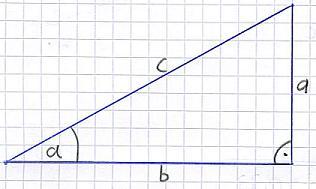
Die Sinus-, Kosinus- und Tangens-Funktion zum Berechnen eines Winkels darf nur an einem rechtwinkligen Dreieck angewendet werden. Die folgende Grafik zeigt euch ein solches Dreieck. Unterhalb findet ihr weitere Informationen dazu:
Sinus, Kosinus und Tangens (Winkelfunktionen) Video:
Dieser Artikel liegt auch als Video vor.
- Hinweise: Dies ist noch ein Tafelvideo. Eine Neuauflage in HD ist geplant. Der Abruf ist auch direkt in der Rubrik Sinus, Kosinus und Tangens (Winkelfunktionen) Video möglich.
- Probleme: Bei Abspielproblemen bitte den Artikel Video Probleme aufrufen.
Ankathete, Gegenkathete und Hypotenuse
Soweit ein Dreieck. An diesem Punkt müsst ihr euch nun ein paar Begriffe merken. Diese tauchen immer wieder bei der Berechnung auf. Zu dem sind ein paar Eigenschaften festzuhalten:
- Rechts, unten im Dreieck wurde ein rechter Winkel eingezeichnet
- Den Winkel links unten bezeichnen wir als α ( gesprochen: Alpha )
- Die Seite "a" wird als Gegenkathete bezeichnet, denn sie liegt gegenüber vom Winkel α
- Die Seite "b" wird als Ankathete bezeichnet, denn sie liegt am Winkel α
- Die Seite "c" wird als Hypotenuse bezeichnet
Die Bezeichnungen Ankathete, Gegenkathete und Hypotenuse sollten euch bereits vom Satz des Pythagoras bekannt sein. Mit diesem Wissen können wir nun Winkel und - falls der Winkel gegeben ist - Längen ausrechnen.
Sinus
Zeit zu rechnen. Dabei beginnen wir mit dem Sinus. Es gilt der folgende mathematische Zusammenhang:
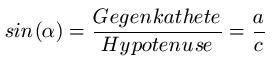
Anmerkungen:
- Für Alpha ( α ) wird ein Winkel in Grad eingesetzt, zum Beispiel 20 Grad oder 40 Grad.
- Die Längen für die Gegenkathete und Hypotenuse müssen in gleichen Einheiten eingesetzt werden, zum Beispiel alles in Meter einsetzen.
- Ihr müsst euren Taschenrechner auf DEG ( Degree ) einstellen, sonst bekommt ihr ein falsches Ergebnis raus.
- Wenn ihr den Winkel ausrechnen wollt, müsst ihr mit arcsin arbeiten ( Siehe Beispiele )
Beispiel 1:
Die Gegenkathete hat eine Länge von 3cm ( a = 3cm ) und die Hypotenuse hat eine Länge von 5cm ( c = 5cm ). Wie groß ist der Winkel α ( Alpha )?
Tabelle nach rechts scrollbar
| Lösung: | |
| sinα = a : c | |
| sinα = 3cm : 5cm | |
| sinα = 0.6 | | arcsin |
| α = 36,87 Grad |
Setzt die Zahlen in die Sinus-Gleichung ein. Danach wird die Division auf der rechten Seite ausgerechnet. Ihr erhaltet sinα = 0.6. Nun kommt der interessante Teil: Um das sin weg zu bekommen, müsst ihr arcsin nutzen. In den Taschenrechner müsst Ihr also arcsin 0,6 eingeben. Es errechnet sich dadurch ein Winkel von 36,87 Grad ( sofern ihr euren Taschenrechner auf Degree stellt ).
Cosinus / Kosinus
Nach dem Sinus kommen wir nun zum Cosinus / Kosinus. Die Formel sieht wie folgt aus:
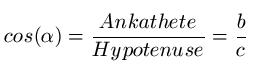
Anmerkungen:
- Für Alpha ( α ) wird ein Winkel in Grad eingesetzt, zum Beispiel 25 Grad oder 45 Grad.
- Die Längen für die Ankathete und Hypotenuse müssen in gleichen Einheiten eingesetzt werden, zum Beispiel alles in Meter einsetzen.
- Ihr müsst euren Taschenrechner auf Degree einstellen, sonst bekommt ihr ein falsches Ergebnis raus.
- Wenn ihr den Winkel ausrechnen wollt, müsst ihr mit arccos arbeiten ( Siehe Beispiele )
Beispiel 2:
Die Ankathete hat eine Länge von 3cm ( b = 3cm ) und die Hypotenuse hat eine Länge von 5cm ( c = 5cm ). Wie groß ist der Winkel α ( Alpha )?
Tabelle nach rechts scrollbar
| Lösung | |
| cosα = b : c | |
| cosα = 3cm : 5cm | |
| cosα = 0.6 | | arccos |
| α = 53,13 Grad |
Setzt die Zahlen in die Cosinus-Gleichung ein. Danach wird die Division auf der rechten Seite ausgerechnet. Ihr erhaltet cosα = 0.6. Nun kommt der interessante Teil: Um das cos weg zu bekommen, müsst ihr arccos nutzen. In den Taschenrechner müsst ihr also arccos 0,6 eingeben. Es errechnet sich dadurch ein Winkel von 53,13 Grad ( sofern ihr euren Taschenrechner auf Degree stellt ).
Tangens
Nach Sinus und Kosinus geht es nun an die Tangens-Funktion. Auch hier zunächst erst einmal die Formel:
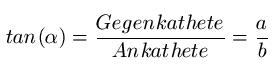
Anmerkungen:
- Für Alpha ( α ) wird ein Winkel in Grad eingesetzt, zum Beispiel 30 Grad oder 50 Grad.
- Die Längen für die Gegenkathete und Ankathete müssen in gleichen Einheiten eingesetzt werden, zum Beispiel alles in Meter einsetzen.
- Ihr müsst euren Taschenrechner auf DEG ( Degree ) einstellen, sonst bekommt ihr ein falsches Ergebnis raus.
- Wenn ihr den Winkel ausrechnen wollt, müsst ihr mit arctan arbeiten ( Siehe Beispiele )
Beispiel 3:
Die Ankathete hat eine Länge von 3cm ( b = 3cm ) und die Gegenkathete hat eine Länge von 3cm ( a = 3cm ). Wie groß ist der Winkel α ( Alpha )?
Tabelle nach rechts scrollbar
| Lösung | |
| tanα = a : b | |
| tanα = 3cm : 3cm | |
| α = 45 Grad | |
Setzt die Zahlen in die Tangens-Gleichung ein. Danach wird die Division auf der rechten Seite ausgerechnet. Ihr erhaltet tanα = 1. Nun kommt der interessante Teil: Um das tan weg zu bekommen, müsst ihr arctan nutzen. In den Taschenrechner müsst ihr also arctan 1,0 eingeben. Es errechnet sich dadurch ein Winkel von 45 Grad ( sofern ihr euren Taschenrechner auf Degree stellt ).
Links:
- Zu den Übungsaufgaben "Sinus-Cosinus-Tangens-Winkel"
- Weiter zu Sinus-Funktion und Kosinus-Funktion ( Schwingungen )
- Zur Trigonometrie-Übersicht
- Zur Mathematik-Übersicht
146 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: