Zahlenstrahl

Mit dem Zahlenstrahl befassen wir uns in diesem Artikel. Zu Beginn geht es mit dem Zahlenstrahl bis 10 los, welcher bereits in Klasse 1 und Klasse 2 der Grundschule behandelt wird. Im Anschluss wird der Zahlenstrahl auf 20, 100 und 1000 ausgedehnt. Der Unterschied zwischen Zahlenstrahl und Zahlengerade wird behandelt und es werden rationale Zahlen (Brüche) auf dem Zahlenstrahl eingetragen. Die Lerninhalte liegen als Text und als Video vor.

Ab der 1. Klasse der Grundschule wird im Mathematik-Unterricht der Zahlenstrahl behandelt. Aber was ist eigentlich ein Zahlenstrahl?

Hinweis:

Ein Zahlenstrahl ist eine gerade Linie auf der Zahlen der Größe nach angeordnet werden. Je weiter auf dem Zahlenstrahl nach rechts gegangen wird, desto größer ist die Zahl. Werden auch negative Zahlen verwendet benutzt man nicht mehr den Begriff Zahlenstrahl, sondern bezeichnet dies als Zahlengerade.

Der Zahlenstrahl bis 10 wird gleich zu Beginn der Grundschule behandelt. Hier werden die natürlichen Zahlen bis 10 aufgetragen. Eine Vorlage für einen Zahlenstrahl bis 10 sieht zum Beispiel so aus:

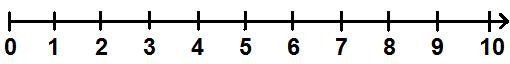
Zahlen bis 10 eintragen:

Im ersten Schritt sollen Schüler und Schülerinnen lernen auf einem Zahlenstrahl Zahlen einzutragen oder diese abzulesen. Die Zahlen können mit Pfeilen markiert werden. Im nächsten Beispiel ist die Zahl 3 mit einem roten Pfeil markiert und die Zahl 8 ist mit einem blauen Pfeil markiert.

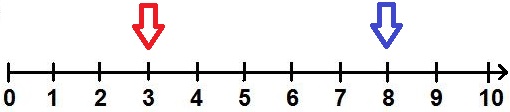
Zahlenstrahl Addition und Subtraktion:

Die Grundrechenarten Addition (+) und Subtraktion (-) lassen sich auch sehr schön am Zahlenstahl zeigen:

• 2 + 6 = 8 bedeutet, dass ich von der 2 um 6 nach rechts gehe und auf der 8 anhalte.
• 7 - 4 = 3 bedeutet, dass ich von der 7 um 4 nach links gehe und auf der 3 anhalte.

Zahlenstrahl bis 20

Werden im Mathematik-Unterricht größere Zahlen bei Addition (+) und Subtraktion(-) behandelt, so wird auch der Zahlenstrahl erweitert. Rechnen Schüler und Schülerinnen im Zahlenraum bis 20 wird auch der Zahlenstrahl bis 20 erweitert. Um nicht zu viele Striche und Zahlen an den Strahl schreiben zu müssen lässt man manchmal jede zweite Zahl weg.

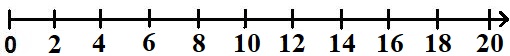
Zahlen bis 20 eintragen:

Auf dem Zahlenstrahl bis 20 können ebenfalls Zahlen eingetragen werden. Im Fall der Zahl 16 kann direkt ein Pfeil auf die entsprechende Zahl zeigen. Ist die Zahl jedoch nicht direkt ablesbar, so muss man sich darüber Gedanken machen, wo diese sich befindet. Die Zahl 5 steht nicht direkt am Zahlenstrahl. Die 5 ist jedoch die natürliche Zahl zwischen 4 und 6. Daher muss sie sich mittig zwischen 4 und 6 befinden.

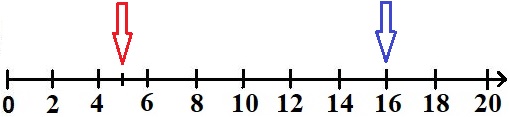
Wie lange ist ein Zahlenstrahl? Eigentlich unendlich lange, denn man kann stets weitere Zahlen anhängen. Auf dem Blatt Papier oder auf dem Monitor gibt es jedoch nur begrenzt Platz. Aus diesem Grund zeichnet man nur einen Teil vom Zahlenstrahl. Der nach rechts gehende Pfeil deutet an, dass der Zahlenstrahl im Prinzip noch weiter geht.

Zahlenstrahl bis 100 und 1000

In der Grundschule wird ebenfalls noch der Zahlenstrahl bis 100 und meistens auch bis 1000 behandelt. Grundsätzlich gilt: Wird der komplette Zahlenstrahl bis zur 100 oder gar 1000 dargestellt, so werden oft nur Zehnerschritte oder Hunderterschritte an die Striche geschrieben. In manchen Fällen wird dann "reingezoomt", spricht es wird nur ein kleiner Abschnitt dargestellt (zum Beispiel von 50 bis 60). Die nächste Grafik zeigt jedoch den ganzen Zahlenstrahl von 0 bis 100 in Zehnerschritten:

Zahlen bis 100 eintragen:

Werden bei einem Zahlenstrahl bis 100 die Zehnerschritte eingetragen, so ist es sehr einfach direkt auf die 40 oder 50 einen Pfeil zu setzen, um diese Zahlen auszuwählen. Liegt die Zahl jedoch zwischen 40 und 50 kann eine feinere Unterteilung vorgenommen werden. In der Mitte zwischen 40 und 50 wird ein Strich gesetzt sowie links und rechts von diesem neuen Strich noch jeweils 4 weitere Striche. Diese Striche stellen jeweils "1 weiter" da. Der Pfeil im nächsten Beispiel zeigt daher auf die 48.

Zahlenstrahl bis 1000:

Der Zahlenstrahl kann beliebig erweitert werden. Die nächste Grafik zeigt den Zahlenstrahl bis 1000, unterteilt in Hunderterschritte.

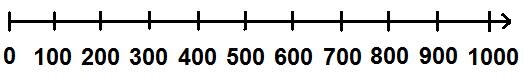
Zahlenstrahl wird zur Zahlengerade

In der Mathematik gibt es nicht nur positive Zahlen (1, 2, 3, 4, ...), sondern auch negative Zahlen (-1, -2, -3, -4, ...). Sollten auch negative Zahlen auf einem Zahlenstrahl eingetragen werden, so muss dieser nach links erweitert werden. In diesem Fall spricht man jedoch nicht mehr von einem Zahlenstrahl, sondern von einer Zahlengerade.

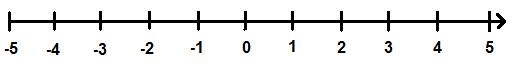
Negative Zahlen markieren:

Selbstverständlich können auch negative Zahlen auf der Zahlengerade markiert werden. Die Pfeile sind damit links der Zahl Null.

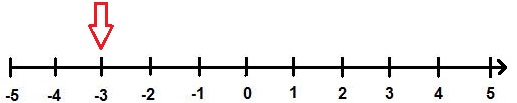
Rechnen mit negativen Zahlen:

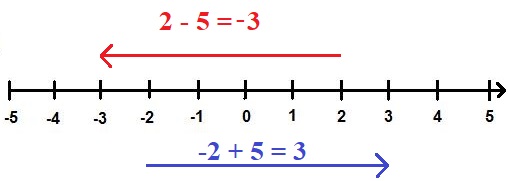
Mit der Zahlengerade lassen sich auch sehr gut Additionen und Subtraktionen im negativen Bereich verstehen:

• 2 - 5 = -3 bedeutet, dass ich von der 2 um 5 nach links gehe auf auf der -3 lande.
• -2 + 5 = 3 bedeutet, dass ich von der -2 um 5 nach rechts gehe und auf der +3 lande.

Rationale Zahlen (Brüche)

Auch rationale Zahlen (Brüche) lassen sich auf einem Zahlenstahl darstellen. Die nächste Grafik zeigt ein solches Beispiel: Dabei soll der Bereich zwischen 0 und 1 in drei gleich große Teile aufgeteilt werden. Dies führt zu 2 Strichen zwischen der 0 und der 1. Da es 3 gleich große Teile gibt, ist der Nenner vom Bruch 3. Die Zähler sind 1 und 2.

Soll der Bruch 1/3 eingetragen werden, so zeigt der Pfeil auf den ersten Strich.

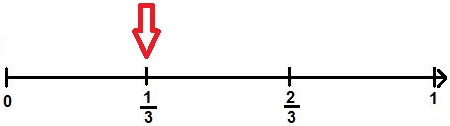
Weiterführende Inhalte:

• Grundlagen Mathematik Übersicht
• Zur Mathematik-Übersicht
• Addition von Zahlen
• Subtraktion von Zahlen
• Vergleichsoperationen: größer, kleiner und gleich
• Nachbarzahlen
• Zahlenreihen
• Gerade Zahlen
• Ungerade Zahlen
• Rechenhaus
• Tauschaufgaben
• Umkehraufgaben
• Zahlenstrahl
• Kettenaufgaben
• Rechentabelle