Elektrisches Netzwerk / Netz berechnen

Wie kann man ein elektrisches Netzwerk berechnen? Genau hierzu sehen wir uns die nötigen Grundlagen und einige Beispiele genauer an. Dabei werden wichtige Grundlagen aus dem Bereich der Elektrotechnik besprochen. Dieser Artikel gehört zu unserem Bereich Elektrotechnik bzw. Physik.

Um elektrische Netzwerke berechnen zu können sind einige Grundlagen der Elektrotechnik wichtig: Das Ohmsche Gesetz, die Knotenregel und die Maschenregel. Mit diesen können wir uns elektrische Netzwerke aus Reihenschaltung, Parallelschaltung und somit Gruppenschaltung ansehen.

Das Ohmsche Gesetz:

Sehen wir uns das wichtigste Gesetz der Elektrotechnik an: Das Ohmsche Gesetz. Wichtig dafür ist: Ein (elektrischer) Widerstand ist genau dann ein ohmscher Widerstand, wenn sein Wert unabhängig von der Stärke des fließenden Stroms, der elektrischen Spannung und der Frequenz ist. Es gilt damit dieser Zusammenhang:

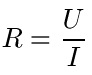
Es gilt:

• "R" ist der Widerstand in Ohm
• "U" ist die Spannung in Volt
• "I" ist der Strom in Ampere

Beispiel 1:

Die Spannung sei 10 Volt, der Strom sei 2 Ampere. Wie groß ist der elektrische Widerstand?

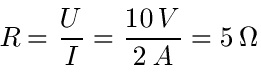
Knotenregel:

Kommen wir als nächstes zur Knotenregel. Diese besagt ganz einfach, dass der Strom, der in einen Knoten reinfließt genauso groß sein muss, wie der Strom, der herausfließt.

• Einfließender Strom = Herausfließender Strom

Beispiel 2:

Drei Ströme fließen in einen Knoten rein, einer fließt raus. Gegeben sei I₁ = 2 A, I₂ = 1 A und I₃ = 4 A. Wie groß ist der Strom I₄?

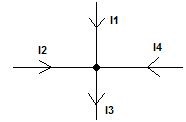
Lösung: Die Ströme I₁, I₂ und I₄ fließen rein und müssen so groß sein wie I₃. Mit der Gleichung erhalten wir I₄ = 1 A.

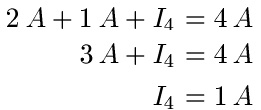
Beispiel 3:

Es folgt ein Auszug aus einem elektrischen Netz. Hier sollen die Ströme I₁ und I₂ berechnet werden.

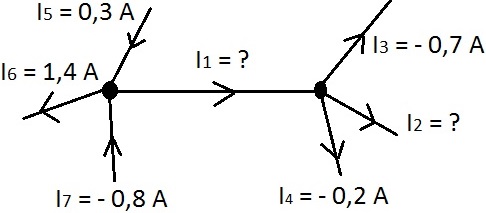
Lösung des Beispiels: Die Pfeile von I₆ sowie I₁ zeigen vom linken Knoten weg, die Pfeile der Ströme I₅ und I₇ zeigen auf den Knoten hin. Die Ströme müssen natürlich gleich groß sein, entsprechend stellen wir die Gleichung auf. Dabei muss beachtet werden, dass wir I₇ mit negativem Vorzeichen einsetzen (der Strom fließt eigentlich raus), uns beim Aufstellen der Gleichung jedoch an der Pfeilrichtung orientieren. Im Anschluss stellen wird die Gleichung für eingehende und ausgehende Ströme für den rechten Knoten auf (ebenfalls unter Beachtung der Pfeilrichtung und mit negativem I₃).

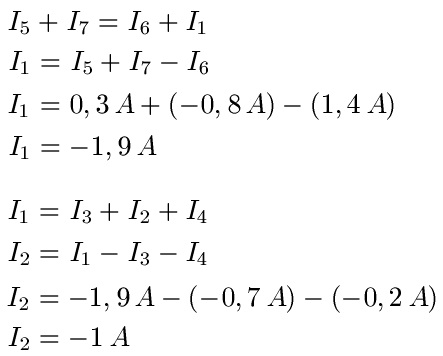
Maschenregel:

Kommen wir noch zur Maschenregel. Die Aussage dabei ist die Folgende:

• Die Summe aller Spannungen innerhalb einer Masche ist gleich Null.

Hinweise:

• Spannungen sind dann positiv, wenn die Umlaufrichtung der Masche in die gleiche Richtung verläuft wie der jeweiligen Spannungszählpfeile (also bei U_R1, U_R2 und U_R3).
• Spannungen sind dann negativ, wenn die Umlaufrichtung der Masche entgegen den jeweiligen Spannungszählpfeilen verläuft (also bei U₀).

Beispiel 4:

Gegeben sei die folgende Schaltung mit drei elektrischen Widerständen und einer Quelle für Spannungen. Wie groß ist U₀?

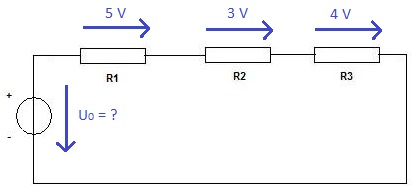
Lösung: Die Spannungen an den drei Widerständen gehen rechts herum und werden daher positiv gezählt. Die Spannung der Quelle läuft in die andere Richtung und wird daher negativ eingesetzt. Die daraus entstehende Gleichung stellen wir nach der Spannung der Quelle U₀ um, setzen die Angaben aus dem Text weiter oben ein und berechnen damit U₀ = 12 V.

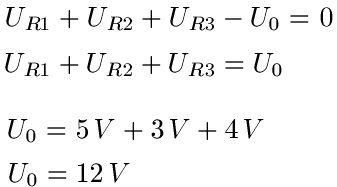
Elektrisches Netzwerk / Netz berechnen

Elektrische Netzwerke bzw. elektrische Netze bestehen aus mehr Bauteilen als wir dies weiter oben behandelt haben. Diese müssen für eine Berechnung zusammengefasst werden. Nun wollen wir mehrere Widerstände hintereinander schalten. Dabei sprich man von Reihenschaltung von Widerständen. Dies kann zum Beispiel so aussehen:

Meist nummeriert man die Widerstände durch. So auch hier in den Grafiken geschehen. Man kann diese drei Widerstände auch zu einem einzigen Zusammenfassen. Dabei addiert man alle Widerstände: R_Gesamt = R₁ + R₂ + R₃. Ob man nun zwei, drei, vier oder mehr Widerstände hintereinander hat, spielt keine Rolle. Einfach alle zusammenaddieren und man hat den Gesamtwiderstand.

Beispiel 5:

Wir wollen den folgenden Stromkreis analysieren und berechnen, wie viel Strom in dem Kreislauf fließt:

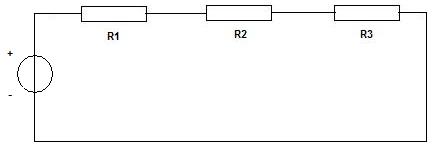
Nehmen wir die folgenden Werte an: R₁ = 200Ω, R₂ = 100Ω, R₃ = 500Ω und die Spannung ist 220 V. Die Frage lautet: Wie viel Strom fließt in den Leitungen? Dazu fassen wir zunächst die Widerstände zu einem Gesamtwiderstand zusammen. R_Gesamt = 200 Ω + 100 Ω + 500 Ω = 800 Ω. Und dies setzen wir in U = R · I ein. Dies liefert: 220 V = 800 Ω · I. Man berechnet somit 220 V dividiert durch 800 Ω. Rechnet man das aus, erhält man I = 0,275 A.

Es kann natürlich passieren, dass Widerstände nicht hintereinander geschaltet werden, sondern parallel zu einander liegen. Das kann dann so aussehen:

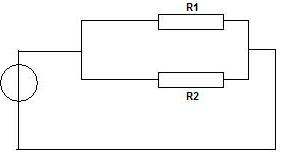
Auch in diesem Fall ist es möglich, die Widerstände zusammen zu fassen. Liegen zwei Widerstände parallel, lautet die Formel.

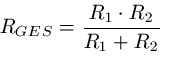
Setzt zum Beispiel für R₁ einmal 100 Ohm ein und für R₂ 200 Ohm ein. Dann solltet ihr R_Gesamt = 66,66 Ohm erhalten. Ausführlich sieht das dann so aus:

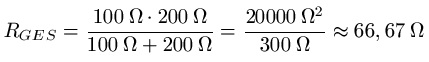
Liegen in einer Schaltung mehr als zwei Widerstände parallel, so verwendet man die folgende Formel zur Berechnung des Gesamtwiderstandes (R_GES).

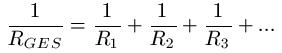
Tipp: Setzt alle Widerstandswerte R₁, R₂... ein und berechnet damit die "rechte" Seite der Gleichung. Im Anschluss nehmt ihr einfach den Kehrwert und erhaltet damit den Gesamtwiderstand. Ihr müsst also - wie aus der Mathematik gewohnt - nach R_GES dann umstellen.

Elektrische Netze: Gruppenschaltung

An einfachen Beispielen möchte ich euch nun zeigen, wie man eine so genannte Gruppenschaltung berechnet. Unter einer Gruppenschaltung versteht man eine elektronische Schaltung, bei der Widerstände sowohl als Reihenschaltung, wie auch als Parallelschaltung vorkommen. Werft dazu einen Blick auf das folgende Beispiel.

Beispiel 6:

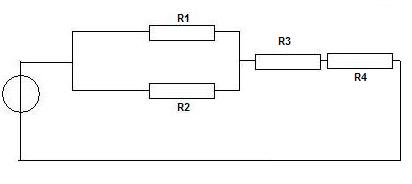
Wie man sehen kann, liegen die Widerstände R₁ und R₂ parallel zu einander. Die Widerstände R₃ und R₄ hingegen liegen als Reihenschaltung vor. Mit dem Wissen zur Reihenschaltung und Parallelschaltung kann man diese nun zusammen fassen. Wir erhalten dadurch die Ersatz-Widerstände R_Vorne und R_Hinten. Dies sieht dann wie folgt aus:

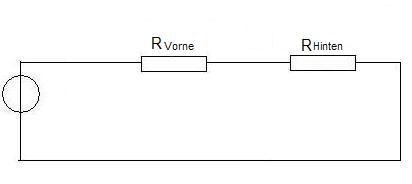
Die Berechnung für R_Vorne und R_Hinten sehen wie folgt aus. Anschließend werden diese beiden in Reihe geschalteten Widerstände wieder zusammen gefasst. Hier die Rechnung:

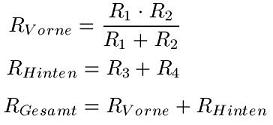
Beispiel 7 mit Zahlen:
Zur besseren Verdeutlichung soll nun das Beispiel noch mit Zahlen gerechnet werden. Für die vier Widerstände setzen wir nun die folgenden Zahlen ein und berechnen damit den Gesamtwiderstand.

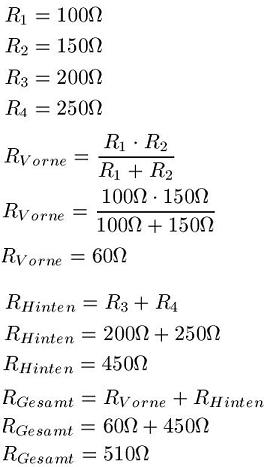
Beispiel 8:

Zeit für ein zweites Beispiel. Hier die Schaltung, deren Gesamtwiderstand berechnet werden soll.

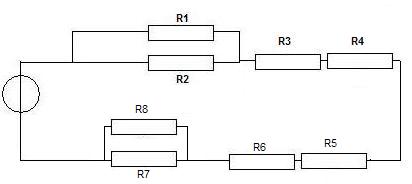
Die Widerstände R₁ und R₂ sowie R₇ und R₈ liegen jeweils parallel zueinander. Alle anderen Widerstände liegen in Reihe zueinander. Den Gesamtwiderstand berechnet man somit wie folgt:

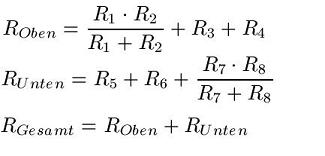
Links:

• Zur Elektrotechnik-Übersicht
• Zur Physik-Übersicht