ggT ▷ größter gemeinsamer Teiler Erklärung

Der größte gemeinsame Teiler - kurz ggT - von zwei Zahlen ist die größte Zahl, durch die du beide Zahlen ohne Rest teilen kannst. Beispiele und einfache Erklärungen mit Teilermengen oder der Primfaktorzerlegung bekommst du hier vorgerechnet. Wir sehen uns den ggT für 2 Zahlen und für 3 Zahlen an. Die Inhalte liegen als Text und als Video vor.

Um den größten gemeinsamer Teiler von zwei Zahlen zu finden suchen wir zunächst die Teiler der beiden Zahlen und schreiben diese in eine Teilermenge. Solltest du noch nicht wissen wie man die Teiler kleiner Zahlen findet, so beschäftigte dich bitte zunächst mit den Inhalten Teiler einer Zahl und den Teilbarkeitsregeln.

Als Beispiel soll der größte gemeinsamer Teiler der Zahlen 25 und 30 gefunden werden. Dazu notieren wir uns zunächst die Teiler der Zahl 25 und die Teiler der Zahl 30 in einer Menge.

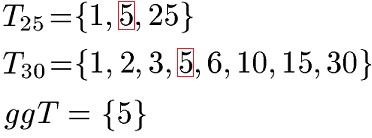
Wir suchen nun die größte Zahl welche in beiden Mengen vorkommt. Für dieses Beispiel ist dies die Zahl 5. Der größte gemeinsame Teiler von 25 und 30 ist damit die 5. Dies kannst du auch mathematisch mit der Schreibweise ggT(25,30) = 5 ausdrücken.

ggT mit Primfaktorzerlegung

Mit der Primfaktorzerlegung lässt sich sehr einfach der größte gemeinsame Teiler von zwei etwas größeren Zahlen bestimmen. Dazu zerlegen wir jede der Zahlen in eine Multiplikation aus möglichst kleinen Zahlen.

Als Beispiel soll das ggT von 32 und 42 gefunden werden. Wir zerlegen die 32 in eine Multiplikation aus der Zahl 2. Wir erhalten die Zahl 2 insgesamt 5 Mal. Daher können wir das mit der Potenzschreibweise 2⁵ abkürzen.

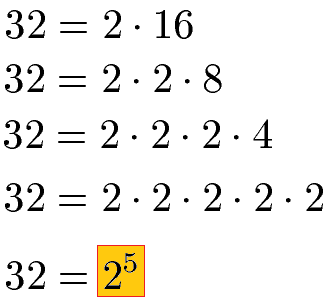
Die Zerlegung der Zahl 32 in möglichst kleine Zahlen bedeutet nichts anderes als eine Zerlegung in Primzahlen. Primzahlen sind Zahlen, die nur durch 1 und durch sich selbst teilbar sind. Solltest du Schwierigkeiten haben Zahlen zu zerlegen, wirf bitte noch einen Blick auf die Teilbarkeitsregeln oder auf die jetzt folgenden Beispiele.

Im nächsten Schritt zerlegen wir die 42 in Primfaktoren mit 2 · 21 und die 21 zerlegen wir in 3 · 7. Auch dies schreiben wir als Potenz.

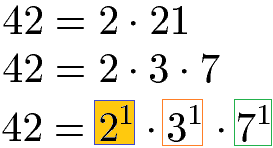
Den größten gemeinsamen Teiler (ggT) finden wir, indem wir die Primfaktoren suchen, welche in beiden Zerlegungen vorkommen und die kleinste Hochzahl haben. Die Basis 2 kommt bei 2⁵ und 2¹ vor. Wir nehmen den kleinere Hochzahl, daher 2¹. Die Basen 3 und 7 kommen nur bei der Zerlegung von 42 vor, jedoch nicht bei der Zerlegung von 32 und fallen daher raus. Der ggT ist damit 2¹ = 2.

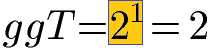
Dies kann auch mit der Schreibweise ggT(32,42) = 2 aufgeschrieben werden.

Größter gemeinsamer Teiler bei 3 Zahlen

Den größten gemeinsame Teiler für 3 Zahlen findet man ebenfalls mit der Primfaktorzerlegung. Dazu werden alle 3 Zahlen in eine Multiplikation aus nur Primzahlen zerlegt. Die Primfaktoren werden als Potenzen geschrieben und die Potenzen für den ggT rausgesucht.

Als Beispiel soll der größte gemeinsame Teiler für die Zahlen 88, 144 und 198 berechnet werden. Dazu zerlegen wir zunächst die 88 in Primfaktoren und schreiben das Ergebnis als Potenz.

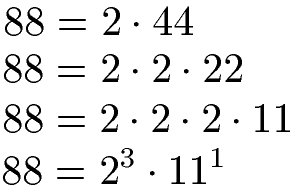
Für die 144 wird ebenfalls eine Primfaktorzerlegung durchgeführt. Auch hier bringen wir das Ergebnis in die Potenzschreibweise:

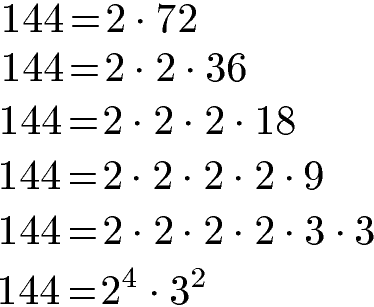
Fehlt noch die dritte Zahl: Die größte der drei Zahlen ist die 198 und kann ebenfalls in eine Multiplikation aus Primzahlen zerlegt werden:

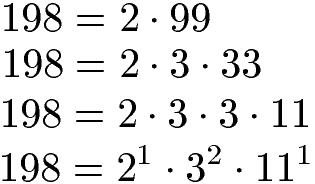
Wir haben für 3 Zahlen die Primfaktorzerlegung durchgeführt. Wie suchen nun die Potenzen mit gleicher Basis raus. Allerdings existiert nur die Potenz mit Basis 2 bei allen drei Zerlegungen. Daher ist nur die Basis 2 für uns interessant. Wir suchen die Potenz mit dem kleinsten Exponenten: Von 2³, 2⁴ und 2¹ hat 2¹ den kleinsten Exponenten. Daher nehmen wir diese Potenz.

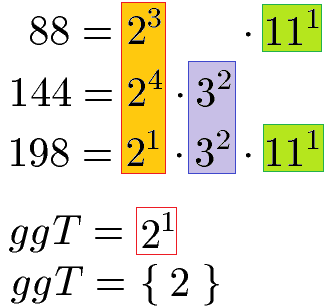
Das ggT von 88, 144 und 198 ist somit 2. Als Schreibweise kann auch ggT(88,144,198) = 2 verwendet werden. Als nächste Themen empfehle ich dir das kleinste gemeinsame Vielfache (kgV) und die Bruchrechnung.