Trapez ▷ Eigenschaften, Flächeninhalt und Umfang

Das Trapez der Mathematik lernst du in diesem Artikel kennen. Für Ungeduldige gibt es zuerst eine kurze Zusammenfassung mit den wichtigsten Informationen zum Trapez. Unterhalb wird das Trapez ausführlich behandelt mit Definition und Eigenschaften, Formeln für den Flächeninhalt sowie Umfang und verschiedene Arten des Trapezes.

Wichtigste Inhalte zum Trapez:

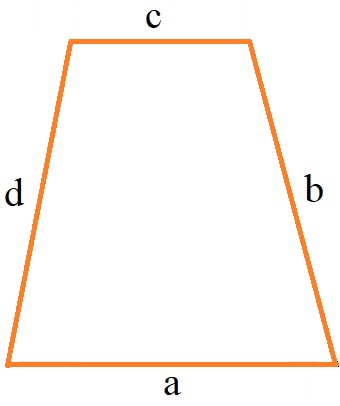
Ein Trapez ist ein Viereck mit einem Paar paralleler Seiten. Die parallelen Seiten des Trapezes werden als Grundseiten bezeichnet, die anderen beiden Seiten als Schenkel. Die vier Eckpunkte werden mit A bis D bezeichnet, die Seiten mit a bis d. Ein Trapez hat 4 Innenwinkel die Alpha, Beta, Gamma und Delta genannt werden.

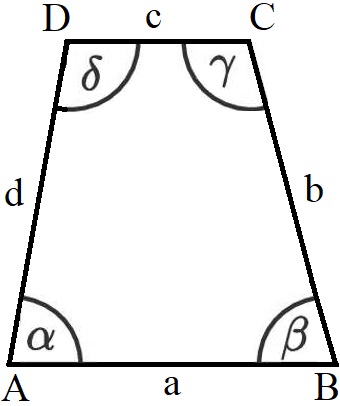
Trapeze können sehr verschieden aussehen. Verschiedene Arten von Trapezen sehen wir uns weiter unten an.

Wichtige Formeln Trapez:

Die wichtigsten Formeln zum Trapez dienen dazu Längen, Flächen und Winkel im Trapez zu berechnen. In Formeln wird der Umfang mit "U" abgekürzt, der Flächeninhalt mit "A". Beispiele zu den Formeln sehen wir uns weiter unten an.

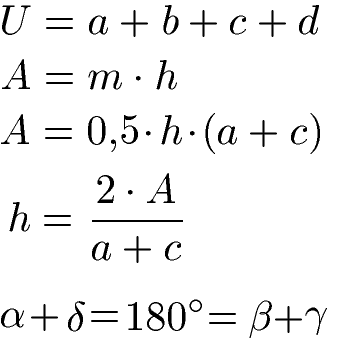
Soweit eine kurze Zusammenfassung zum Trapez. Einzelne Punkte und Beispiele sehen wir uns in den nächsten Abschnitten an.

Trapez Merkmale und Eigenschaften

Ein Trapez hat die folgenden Merkmale bzw. Eigenschaften:

• Ein Viereck, es gibt 4 Ecken.
• Mindestens zwei parallele Seiten.
• Begrenzung durch 4 Seiten.
• Es gibt 4 Innenwinkel mit in Summe 360 Grad.
• Die parallelen Seiten werden als Grundseiten bezeichnet.
• Der Abstand der Grundseiten wird Höhe genannt.

Die Beschriftung eines Trapezes wird wie folgt durchgeführt:

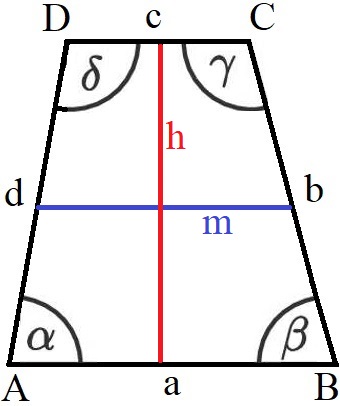
Die Seiten und Winkel der letzten Grafik werden in Formeln zum Trapez verwendet.

Flächeninhalt Trapez mit Formel

Es gibt zwei Möglichkeiten den Flächeninhalt von einem Trapez zu berechnen:

• Mit Höhe und Mittellinie.
• Mit den Seitenlängen a und c und der Höhe h.

Die nächste Grafik zeigt noch einmal welche Angaben verwendet werden um die Fläche von einem Trapez berechnen zu können.

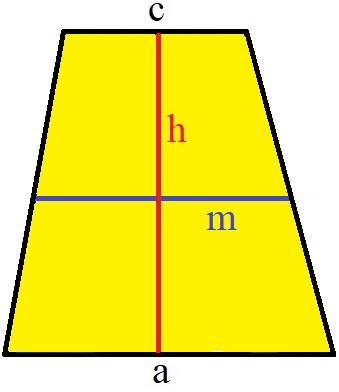
Beispiel Flächeninhalt mit Mittellinie und Höhe:

Ist die Mittellinie 4 Meter lang und die Höhe des Trapezes 5 Meter ergibt sich ein Flächeninhalt von 20 Quadratmetern.

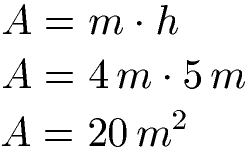
Beispiel Flächeninhalt mit Grundseiten und Höhe:

Ein Trapez hat eine Höhe von 4 Metern und die Grundseiten sind 3 Meter und 2 Meter lang. Mit der Formel zum Flächeninhalt ergibt sich dadurch eine Fläche von 10 Quadratmetern. Beachte bei der Berechnung zuerst die Klammer auszurechnen.

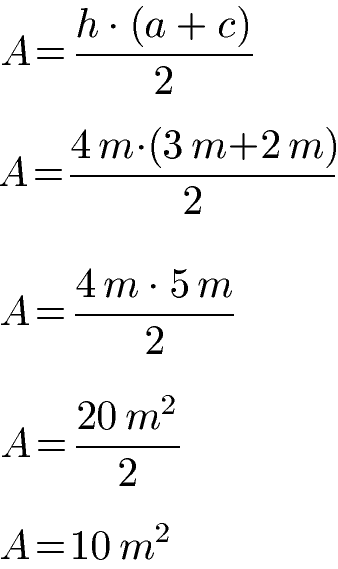
Umfang Trapez mit Formel

Der Umfang von einem Trapez entspricht der Summe der 4 Seitenlängen. Die Länge der Seiten a, b, c und d muss addiert werden um den vollständigen Umfang von einem Trapez zu berechnen.

Trapez Umfang Beispiel:

Die Seitenlängen von einem Trapez seien a = 4 m, b = 2 m, c = 3 m und d = 2 m. Wie groß ist der Umfang? Hinweis: Dazu setzen wir die Angaben in die Formel zur Berechnung des Umfangs ein und erhalten 11 Meter als Gesamtumfang.

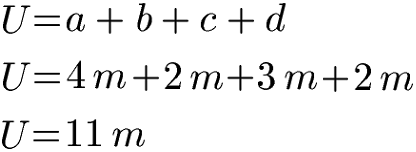
Trapez berechnen mit Formeln

Mit den Formeln zum Trapez lassen sich der Flächeninhalt A, der Umfang U, die Höhe h und die Innenwinkel des Trapezes berechnen. Achte beim Einsetzen der Angaben darauf alles in gleichen Einheiten einzusetzen, zum Beispiel alles in Meter.

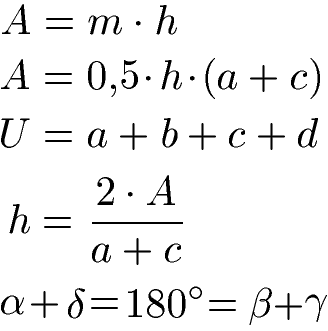
Sofern dir nicht klar ist, wofür die einzelnen Längenangaben stehen bzw. wo sich die Winkel befinden, kannst du einen Blick auf die nächste Grafik werfen.

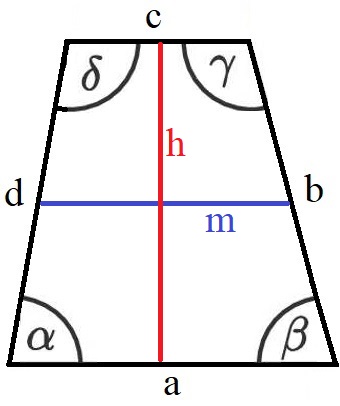
Beispiele zum Flächeninhalt und Umfang eines Trapezes findest du weiter oben. Zur Ergänzung werfen wir noch einen Blick auf das Rechnen mit Winkeln am Trapez.

Beispiel Trapez Innenwinkel:

Der Winkel Delta ist 100 Grad groß. Wie groß ist der Winkel Alpha? Zur Lösung musst du wissen, dass Alpha und Delta gemeinsamen 180 Grad groß sind. Dies ergibt ein Alpha-Winkel von 80 Grad.

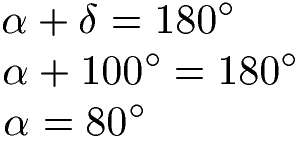
Trapez Volumen:

Das Trapez selbst ist ein zweidimensionales, ebenes Viereck. Aus diesem Grund hat ein Trapez kein Volumen.

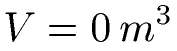
Ein Trapez kann als Grundlage für ein räumliches Gebilde verwendet werden. Ohne diese Erweiterung ist jedoch das Volumen Null.

Trapez Arten

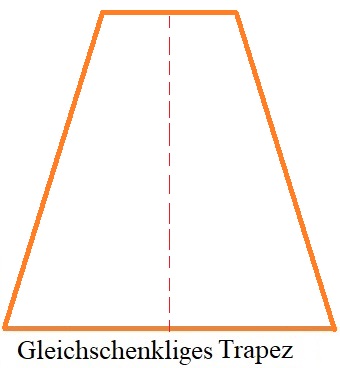
Es gibt verschiedene Arten von Trapezen. Sehr häufig behandelt wird das gleichschenklige Trapez, auch symmetrisches Trapez genannt. Dabei handelt es sich um ein Viereck bei dem zwei gegenüberliegende Seiten parallel sind (in der nächsten Grafik oben und unten. Die beiden anderen Seiten sind gleich lang und verbinden die Grundseiten. Dieses Trapez ist symmetrisch, denn in der Mitte kann es gespielt werden.

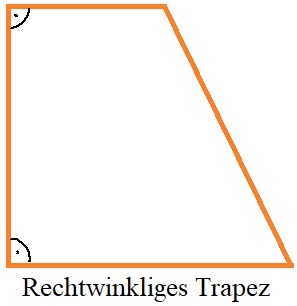
Ein rechtwinkliges Trapez hat zwei rechte Winkel, die nebeneinander liegen. Es wird auch orthogonales Trapez genannt. Ein Spezialfall ist ein rechtwinkliges Trapez mit 4 rechten Winkeln, auch als Rechteck bekannt.

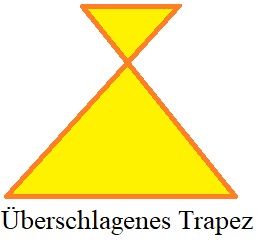
Ein Sonderfall ist das überschlagene Trapez oder auch verschränkte Trapez. Bei diesem schneiden sich die Seiten des Trapezes zu einem gemeinsamen Punkt.