Flächeninhalt Dreieck berechnen

Du lernst in diesem Artikel wie man den Flächeninhalt von einem Dreieck berechnet. Im einfachsten Fall geht dies mit Grundseite mal Höhe. Schwierige Fälle wie das Berechnen des Flächeninhaltes ohne Höhe bzw. mit Winkel oder die Berechnung der Fläche durch den Umfang des Dreiecks sehen wir uns ebenfalls an.

Wichtige Inhalte Zusammenfassung:

Ein Dreieck wird von 3 Seiten begrenzt die mit "a", "b" und "c" bezeichnet werden. Die Seite "c" wird dabei als Grundseite bezeichnet. Auf der Grundseite steht die Höhe "h", die bis in die Spitze des Dreiecks ragt.

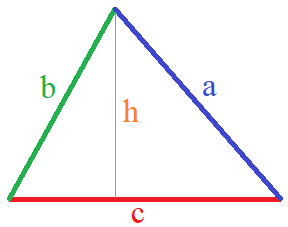
Der Flächeninhalt "A" von einem Dreieck lässt sich durch Multiplikation von Grundseite mal Höhe geteilt durch 2 berechnen.

In der Formel zur Fläche des Dreiecks wird die Grundseite oft mit "c" und die Höhe mit "h" abgekürzt.

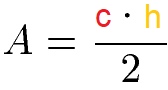
Beispiel Flächeninhalt Dreieck:

Ist die Grundseite des Dreiecks 4 Meter lang (c = 4 m) und die Höhe 3 Meter (h = 3 m) ergibt sich eine Fläche von 6 Quadratmetern.

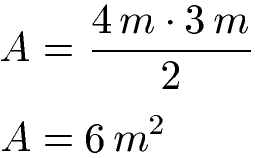
In vielen Fällen ist die Berechnung vom Flächeninhalt jedoch deutlich schwieriger. Im nächsten Schritt sehen wir und verschiedene Formeln zur Berechnung vom Flächeninhalt eines Dreiecks an, gefolgt von Beispielen.

Dreieck Flächeninhalt: Formel Übersicht

Der Flächeninhalt eines Dreiecks lässt sich mit Formeln auf verschiedenen Wegen berechnen:

1. Mit der Grundseite und der Höhe.
2. Mit Winkel und einer Seitenlänge.
3. Mit dem Umfang des Dreiecks und den Seitenlängen.

Die Formeln zur Berechnung des Flächeninhaltes beziehen sich auf die nächste Grafik mit den den Seiten "a", "b" und "c" sowie der Höhe "h" und den Winkeln Alpha, Beta und Gamma.

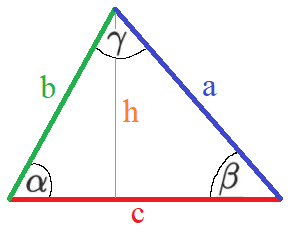
Im einfachsten Fall kann der Flächeninhalt des Dreiecks mit der Länge der Grundseite "c" und der Höhe "h" berechnet werden.

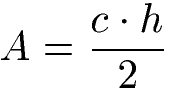
Höhe berechnen Formel:

Kennst du die Höhe vom Dreieck nicht, kannst du diese Höhe eventuell über einen Winkel und eine Seitenlänge berechnen. Ein Beispiel zur Berechnung der Höhe mit Sinus und des Flächeninhaltes findest du weiter unten.

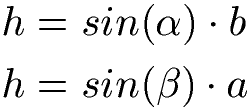
Fehlt dir ein Winkel für die Berechnung des Dreiecks, kannst du diese Formeln verwenden:

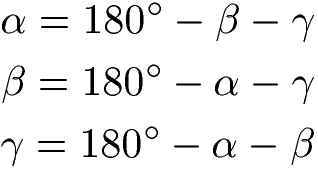
Flächeninhalt durch Umfang:

Eine weitere Möglichkeit besteht darin die Fläche über die Seitenlängen "a", "b" und "c" zu berechnen. Dazu wird zunächst der Umfang des Dreiecks berechnet, indem diese drei Seitenlängen addiert werden. Dieser Umfang wird halbiert und ergibt die Länge "s".

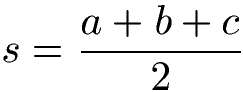
Mit der Hilfe von "s" und den drei Seitenlängen lässt sich ebenfalls der Flächeninhalt des Dreiecks berechnen.

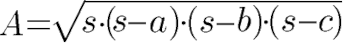
Diese Art der Flächenberechnung über den Umfang wird Satz des Heron genannt. Ein Beispiel findest du weiter unten.

Rechtwinkliges Dreieck Flächeninhalt

Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich aus Breite mal Höhe geteilt durch 2. Die Formel und das Beispiel beziehen sich auf ein Dreieck mit den Seitenlängen "a", "b" und "c" wie in der nächsten Grafik dargestellt.

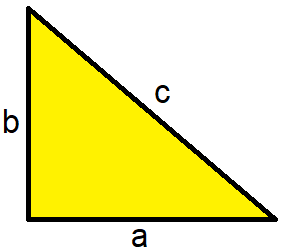
Die Formel zur Berechnung des Flächeninhaltes sieht vor die Längen "a" und "b" miteinander zu multiplizieren und durch 2 zu teilen. Dies ergibt den Flächeninhalt "A".

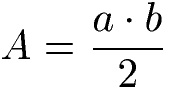
Als Beispiel soll a = 5 m und b = 3 m sein. Die Fläche ergibt damit 7,5 Quadratmeter.

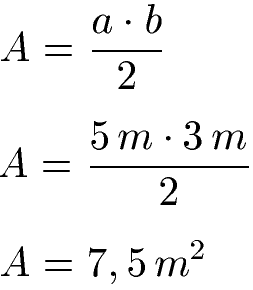
Höhe und Fläche berechnen mit Winkel und Sinus

Die Höhe des Dreiecks kann berechnet werden wenn ein Winkel und eine Seite bekannt sind. Als Beispiel sei der Winkel Alpha mit 60 Grad gegeben und die Seitenlänge b = 5 m. Die Grafik veranschaulicht dies.

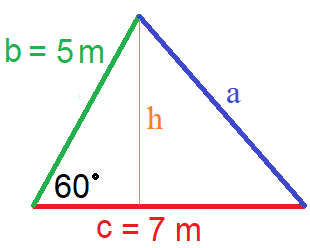
Um die Höhe "h" zu berechnen wird Alpha mit 60 Grad und b = 5 m in die folgende Gleichung eingesetzt. Den Sinus von 60 Grad berechnest du mit dem Taschenrechner. Der Taschenrechner muss in der Einstellung "DEG" stehen für Degree, sonst wird der Sinus für diese Anwendung falsch berechnet.

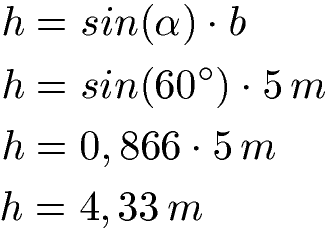
Mit der Höhe von h = 4,33 m gehen wir in die normale Formel zur Berechnung des Flächeninhaltes mit Grundseite mal Höhe geteilt durch 2.

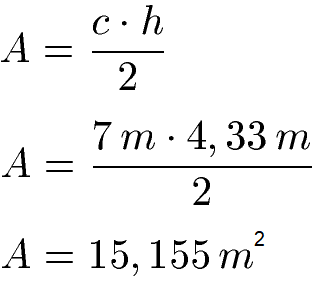
Der Flächeninhalt dieses Dreiecks beträgt 15,155 m².

Dreieck Fläche mit 3 Seiten

Der Flächeninhalt eines Dreiecks kann mit 3 Seiten berechnet werden. Die Berechnung erfolgt mit dem Satz des Heron. Als Beispiel dient ein Dreieck wie in der nächsten Grafik dargestellt mit a = 18 m, b = 16 m und c = 21 m.

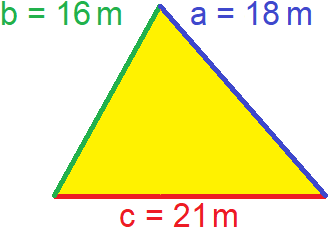
Um den Flächeninhalt mit 3 Seiten zu berechnen, ermitteln wir zunächst den Umfang des Dreiecks. Der Umfang ist die Summe der drei Seitenlängen. Der Umfang wird halbiert und ergibt die Länge "s".

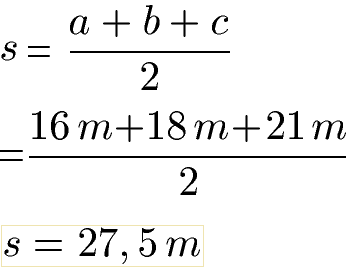
Mit den Seitenlängen "a", "b", "c" und "s" gehen wir in die Formel zum Satz des Heron. Die vier Längen werden eingesetzt und gerechnet. Beachte dabei zuerst die Klammer zu berechnen.

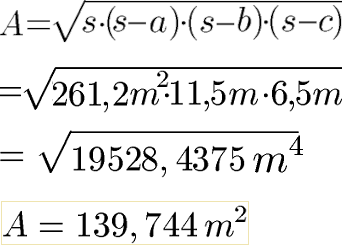
Das Dreieck hat einen Flächeninhalt knapp 140 Quadratmetern.