Dreisatz rechnen ▷ Proportional und Antiproportional

Den Dreisatz behandeln wir in diesem Artikel. Du lernst Schritt für Schritt den proportionalen Dreisatz und den antiproportionalen Dreisatz. Mit Beispielen und Formeln zeige ich dir wie man den Dreisatz rechnet. Als Zusatz gibt es am Ende des Artikels den Dreisatz für die Prozentrechnung.

Der Dreisatz dient dazu mit drei gegebenen Größen eine vierte Größe zu zu berechnen. Der Dreisatz wird in drei Zeilen angegeben.

Beispiel Dreisatz:

5 Kugeln Eis kosten 10 Euro. Was kosten 3 Kugeln Eis? Zur Lösung schreiben wir in die 1. Zeile den bekannten Zusammenhang: 5 Kugeln kosten 10 Euro. In der zweiten Zeile rechnen wir den Preis für eine Kugel Eis aus, daher teilen wir durch 5. Wir suchen den Preis für 3 Kugel, daher multiplizieren wir für die dritte Zeile mit 3.

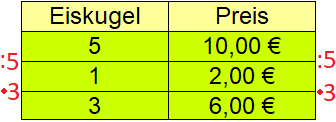
Die Tabelle zum Dreisatz als Text:

• Erster Satz: 5 Kugeln Eis kosten 10 Euro.
• Zweiter Satz: 1 Kugel Eis kostet 2 Euro.
• Dritter Satz: 3 Kugeln Eis kosten 6 Euro.

In den nächsten Abschnitten sehen wir uns verschiedene Arten von Dreisätzen an. Du bekommst außerdem Beispiele zum Dreisatz erklärt und mit Formeln vorgerechnet.

Einfacher Dreisatz berechnen (mit Formel)

Der einfache Dreisatz wird auch als proportionaler Dreisatz bezeichnet. Beim proportionalen Dreisatz gilt die Regel: Je mehr, desto mehr. Beispiel: Für je mehr Personen ich kochen muss, desto mehr Essen muss ich einkaufen. Es gibt zwei Möglichkeiten den proportionalen Dreisatz zu berechnen: Mit einer Tabelle oder mit einer Formel.

Proportionaler Dreisatz Tabelle:

Als Beispiel dient ein Kochrezept: Für 6 Personen werden 372 Gramm Butter benötigt. Es soll jedoch für 9 Personen gebacken werden. Wie viel Butter wird benötigt? Zur Lösung schreiben wir in die erste Zeile die gegeben Informationen: 6 Personen mit 372 Gramm. In der zweiten Zeile rechnen wir auf 1 Person runter, daher Personenzahl und Buttermenge durch 6 teilen. Wir suchen jedoch das Ergebnis für 9 Personen, daher multiplizieren wir die Anzahl der Personen und die Menge an Butter mit 9.

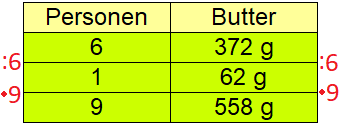
Proportionaler Dreisatz Formel:

Der proportionale Dreisatz kann mit einer Formel berechnet werden. Das Ergebnis (x) ist dabei die Ausgangsmenge (A_M) geteilt durch die Anzahl (A_Z) multipliziert mit der Endzahl (E_Z).

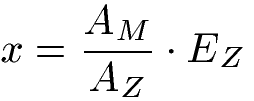
Für unser Beispiel ist die Ausgangsmenge 372 g bei einer Anzahl von 6 Personen. Die Endzahl der Personen ist 9. Mit dieser Formel zum proportionalen Dreisatz lässt sich damit ebenfalls die Endmenge x von 558 Gramm Butter berechnen.

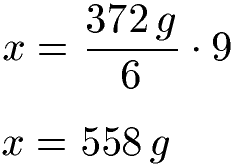
Die bisherigen Beispiele waren von der Art her einfache Dreisätze oder proportionale Dreisätze. In der Mathematik unterscheidet man jedoch verschiedene Arten von Dreisätzen.

Zwei Arten von Dreisatz:

• Einfacher Dreisatz: Der einfache Dreisatz wird auch als proportionaler Dreisatz bezeichnet. Bei diesem gilt: Je mehr, desto mehr. Beispiel: Je mehr Tafeln Schokolade du kaufst, desto mehr Geld kostet der Einkauf.
• Antiproportionaler Dreisatz: Der antiproportionale Dreisatz wird auch umgekehrter Dreisatz genannt. Hier gilt: Je mehr, desto weniger. Beispiel: Je mehr Handwerker arbeiten, desto schneller ist der Raum gestrichen.

Noch verwirrt? Sehen wir uns ein Beispiel zum antiproportionalen Dreisatz an.

Antiproportionaler Dreisatz mit Formel

Der antiproportionale Dreisatz wird auch als umgekehrter Dreisatz bezeichnet. Hier gilt: Je mehr, desto weniger. Beispiel: Je mehr Pumpen ich verwende, desto weniger Zeit benötige ich um einen Keller leer zu pumpen.

Beispiel: Antiproportionale Dreisatz Tabelle

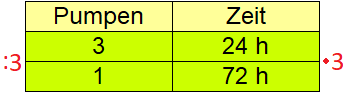
Ein Keller ist mit Wasser vollgelaufen und soll wieder leer gepumpt werden. Dabei würden 3 Pumpen 24 Stunden Zeit benötigen. Wie lange benötigen 8 Pumpen um den Keller zu leeren? Zur Lösung schreiben wir in die 1. Zeile erst einmal die Ausgangsinformation: 3 Pumpen brauchen 24 Stunden.

Im nächsten Schritt wird berechnet, wie lange eine Pumpe für den Keller benötigt. Ab der 2. Zeile wird die Antiproportionalität deutlich. Je mehr Pumpen, desto weniger Zeit wird benötigt. Daher wird die Anzahl der Pumpen durch 3 geteilt, die Zeit wird dadurch jedoch 3 Mal länger. Aus 24 Stunden bei 3 Pumpen werden 72 Stunden bei 1 Pumpe.

Für die 3. Zeile der Tabelle interessieren wir uns jedoch für die Arbeitszeit von 8 Pumpen. Von 1 auf 8 Pumpen bedeutet mit 8 multiplizieren. Für die Zeit bedeutet dies jedoch durch 8 zu teilen.

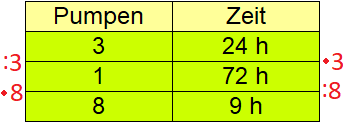
Während eine Pumpe 72 Stunden braucht, benötigen 8 Pumpen nur 9 Stunden.

Beispiel: Antiproportionaler Dreisatz Formel

Der antiproportionale Dreisatz kann ebenfalls mit einer Formel berechnet werden. Dazu wird der Anfangswert (A_W) mit der Anfangszahl (A_Z) multipliziert und durch die Endzahl (E_Z) geteilt. Die Formel berechnet x, sprich das Ergebnis.

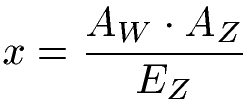
Für das Beispiel haben wir bei der Zeit einen Anfangswert von 24 Stunden bei 3 Pumpen als Anfangszahl. Die Endzahl liegt hingegen bei 8 Pumpen.

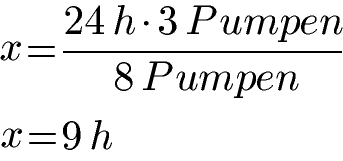
Wir erhalten eine Dauer von 9 Stunden um den Keller leer zu Pumpen.

Dreisatz Prozent: Prozentrechnung mit Formel

Aufgaben zur Prozentrechnung können oftmals per Dreisatz berechnet werden. Im Gegensatz zu normalen Aufgaben zum proportionalen und antiproportionalen Dreisatz wird nicht auf 1 Stück (1 Person, 1 Pumpe, 1 Kugel Eis) runter gerechnet, sondern auf 1 Prozent.

Beispiel: Dreisatz und Prozentrechnung

In einem Jahrgang kommen 40 Schüler zu Fuß in die Schule. Dies sind 25 Prozent aller Schüler. Wie viele Schüler gibt es in diesem Jahrgang?

Zur Lösung notieren wir Gegebenes in der 1. Zeile: 25 Prozent sind 40 Schüler. Wir rechnen von 25 Prozent auf 1 Prozent runter. Dies bedeutet durch 25 zu teilen, was wir rechnerisch ebenfalls bei den Schülern tun.

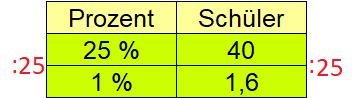
Ein Anteil von 1 Prozent entspricht rechnerisch 1,6 Schülern. Wir interessieren uns jedoch für alle Schüler - also 100 Prozent aller Schüler. Daher multiplizieren wir mit 100.

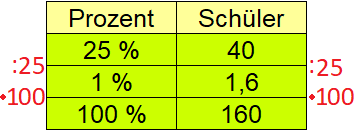
In den Jahrgang gehen 160 Schüler.

Proportional und Antiproportional erkennen

Woran erkennst du, ob du den proportionalen und antiproportionalen Dreisatz anwenden musst? Lösung: Denke über die Aufgabenstellung noch und überlege welcher der beiden Fälle vorliegt.

• Proportionalität: Je mehr, desto mehr:
  • Je mehr Schokolade ich kaufe, desto mehr Geld muss ich ausgeben
  • Je mehr Papier ich kaufe, desto mehr Geld muss ich ausgeben.
• Antiproportionalität: Je mehr, desto weniger:
  • Je mehr Personen bei der Rodung des Waldes helfen, desto weniger Zeit nimmt dies in Anspruch.
  • Je mehr Personen einen Gewinn erhalten, desto weniger erhält die einzelne Person.

Links:

• Übungen: Dreisatz
• Zur Mathematik-Übersicht