PQ Formel für quadratische Gleichungen

Dieser Abschnitt beschäftigt sich mit dem Einsatz der PQ-Formel zum Lösen von quadratischen Gleichungen. Dabei zeigen wir euch zunächst, was eine quadratische Gleichung überhaupt ist und wofür man die PQ-Formel benötigt. Neben Texterklärungen gibt es - wie immer - auch einige Beispiele zur Ansicht.

Zunächst stellt sich natürlich die Frage: Was ist eine quadratische Gleichung? Nun, dabei handelt es sich um eine Gleichung der Form ax² + bx + c = 0 oder eine Gleichung die man auf diese Form bringen kann. Dabei sind a, b und c irgendwelche Zahlen wobei a ungleich Null sein muss. Beispiele: 3x² + 5x + 3 = 0 oder x² + 2x + 1 = 0.

Im Gegensatz zu den Gleichungen, die wir bisher kennen gelernt hatten ( Beispiel: x + 5 = 0 ) ist hier noch ein quadratischer Anteil vorhanden. Wie also löst man nun diese Gleichung nach x auf? Die Antwort auf diese Frage lautet PQ-Formel, mit der wir uns in diesem Abschnitt beschäftigen möchten. Zuvor allerdings noch der Hinweis, auf die benötigen Vorkenntnisse. Für alle, die noch Probleme mit normalen Gleichungen oder der Wurzelrechnung haben, empfehle ich die beiden folgenden Artikel. Alle anderen können gleich mit der PQ-Formel loslegen.

• Gleichungen lösen
• Wurzel-Rechnung

PQ-Formel einsetzen

Um eine Gleichung wie z.B. x² + 2x + 1 = 0 nach x aufzulösen, setzen wir im nun Folgenden die PQ-Formel ein. Ich gebe euch nun erst einmal die Formel an sowie ein paar allgemeine Informationen. Keine Panik: Einige Beispiele erläutern dies im Anschluss.

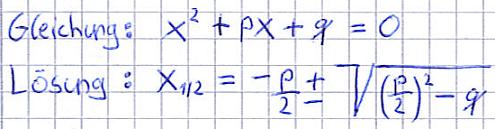
So löst man eine quadratische Gleichung:

1. Bringt die Gleichung in die Form x² + px + q = 0
2. Findet "p" und "q" raus
3. Setzt dies in die PQ-Formel ein
4. Berechnet die Lösung damit

Soviel zur Theorie. Zeit dies Anhand von ein paar Beispielen zu klären. Verfolgt diese Beispiele anhand der 4-Punkte-Liste von eben.

Wichtiger Hinweis: Um Schüler nicht gleich mit vielen Brüchen zu verwirren wurde bei einigen Beispielen gerundet.

Beispiel 1:

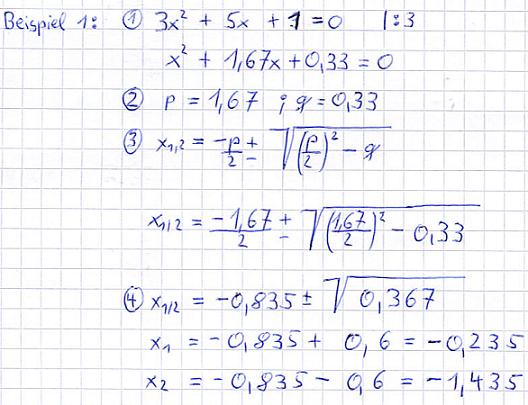
Erläuterungen: Die "3" vor dem x² stört! Dort muss immer eine "1" stehen, sprich 1x². Um dies zu erreichen, wird durch 3 dividiert. Danach werden p und q abgelesen. Die Zahlen von p und q werden in die PQ-Gleichung eingesetzt. Danach wird der Ausdruck vor und unter der Wurzel berechnet. Anschließend wird die Wurzel aus dem Wert gezogen und es wird einmal addiert und einmal subtrahiert. Eine quadratische Gleichung hat maximal zwei Lösungen im reellen.

Beispiel 2:

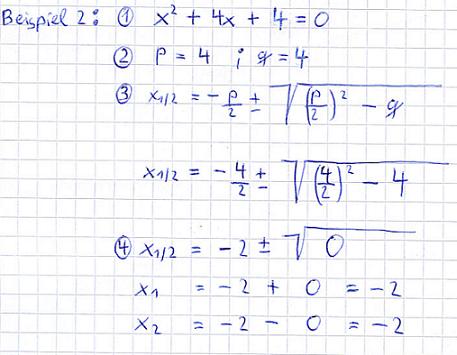
Erklärungen: Die ursprüngliche Aufgabe ist bereits in der richtigen Form. Deshalb kann p und q gleich bestimmt werden. Diese dann in die Gleichung einsetzen und ausrechnen. Wie ihr am Ergebnis seht, gibt es die Lösung -2 doppelt, sprich x₁ = -2 und x₂ = -2.

Hinweis:
Für euch steht eine Klausur an, bei der auch die PQ-Formel vorkommt? Ihr möchtet sehen, ob ihr diese anwenden könnt? Dann solltet ihr noch unsere Aufgaben / Übungen zu diesem Thema machen.

• Zur ersten Aufgabe

PQ Formel: Negative Wurzel / Vorzeichenbeachtung

Es gibt noch zwei kleine Hinweise bei der Berechnung von quadratischen Gleichungen mit der PQ-Formel von uns:

1. Wenn ihr die Zahlen unter der Wurzel berechnet und dann eine negative Zahl unter der Wurzel steht, dürft ihr abbrechen. Dann hat die Gleichung keine Lösung ( zumindest nicht für Schüler, Studenten müssen dann mit imaginären Rechnen ).
2. Achtet auf das Vorzeichen! Habt ihr zum Beispiel die Aufgabe x² -5x + 3 = 0 zu lösen, dann ist p=-5. Diese -5 müsst ihr dann auch in der PQ-Formel einsetzen!

Für beide Fälle findet ihr hier noch jeweils ein Beispiel:

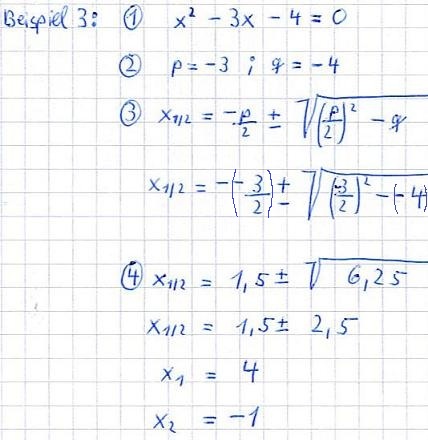
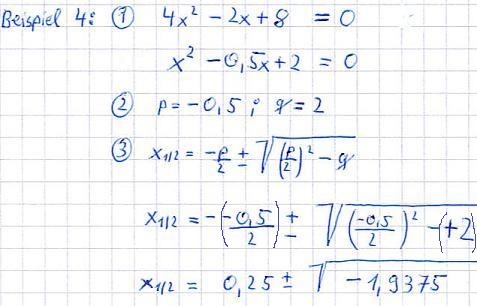
Nur durch sorgfältiges Üben von Aufgaben könnt ihr sicher im Umgang mit der PQ-Formel werden. Deshalb raten wir euch, unsere Übungsaufgaben zum Lösen quadratischer Gleichungen zu rechnen.

Links:

• Zu den Übungen "PQ-Formel"
• Zurück zur Mathematik-Übersicht