Aufleiten Fläche zwischen Funktionen

In diesem Abschnitt nutzen wir die Aufleitung von Funktionen zur Bestimmung von Flächen zwischen zwei Funktionsgraphen. Dabei zeigen wir euch anhand einer Grafik zunächst, was damit gemeint ist und wie man die so genannten Schnittpunkte ausnutzt. Dieser Artikel gehört zu unserem Bereich Mathematik Oberstufe.

Zunächst ein wichtiger Hinweis: Die Begriffe "Aufleiten" bzw. "Aufleitung" sind umgangssprachlich. Sie werden von vielen Schülern einfach als das Gegenteil von Ableiten angesehen. In der Mathematik spricht man bei diesem Bereich richtigerweise von Integration bzw. von Integrationsregeln. Dieser Artikel hier richtet sich also mehr an Schüler bzw. Studenten, die sich der Sache von der Umgangssprache her genähert haben. Für die Berechnung macht dies letztlich natürlich keinen Unterschied.

Fläche zwischen Funktionen durch Aufleitung

Zur Erinnerung: Mit der Integralrechnung - also dem Aufleiten - lässt sich die Fläche unter einer Funktion bestimmen. Mit diesem Wissen versuchen wir im nun Folgenden für ein einfaches Beispiel die Fläche zwischen den Graphen zweier Funktionen zu berechnen. Um das verstehen zu können, sehr euch erst einmal die folgende Grafik an. Beachtet dabei die Verläufe von f(x) und g(x), die grüne Fläche und x₁ sowie x₂.

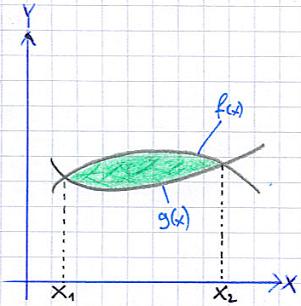
Folgendes gibt es bei dieser Grafik zu verstehen:

• Wir haben zwei Funktionen, die mit f(x) und g(x) bezeichnet werden
• Diese beiden Funktionsgraphen schneiden sich in den Punkten x₁ und x₂
• Die grüne Fläche ist die Fläche, welche die beiden Funktionsgraphen einschließen
• Die Funktion f(x) liegt zwischen den Schnittpunkten stets oberhalb von g(x)

Überlegung: Berechnen wir die Fläche unter g(x) und addieren die grüne Fläche drauf, erhalten wir die Fläche unter f(x). Oder anders ausgedrückt: Berechnen wir die Fläche unter f(x) und ziehen die Fläche unter g(x) ab, erhalten wir die grün eingezeichnete Fläche.

WICHTIG: Es bringt bei der Berechnung von Flächen zwischen Funktionsgraphen gar nichts, einfach irgendwelche Formeln stur auswendig zu lernen. Die Aufgaben können so verschieden gestellt werden, dass ihr mit bloßen Einsetzen in irgend eine Formel schnell zum falschen Ergebnis kommen würdet. Abhilfe schafft eigentlich immer eine Zeichnung der beiden Funktionsverläufe sowie die Berechnung von Schnittpunkten.

Beispiele für Flächenberechnung durch Aufleitung

Im nun Folgenden schauen wir uns verschiedene Beispiele zur Berechnung der Flächen durch Aufleiten an. Für das erste Beispiel geben wir dafür auch eine Beispielrechnung an. Für die anderen Beispiele beschränken wir uns vorerst auf die Idee zur Berechnung der Flächen.

Beispiel 1 zur Fläche durch Aufleitung:

Die Fläche zwischen zwei Funktionsgraphen soll berechnet werden. Deren Gleichungen lauten f(x) = x² - 8x + 17 und g(x) = -x + 7. Zur besseren Übersicht wurde eine Skizze angefertigt:

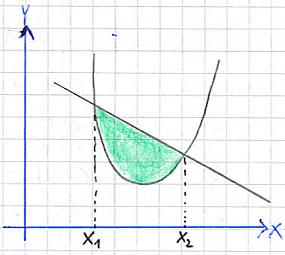
Um die Integrationsgrenzen zu ermitteln, müssen wir die Schnittpunkte der beiden Funktionsgraphen finden. Danach berechnen wir die Flächen unter den jeweiligen Funktionsgraphen. Deren Differenz ist die gesuchte Fläche. Das sieht dann so aus:

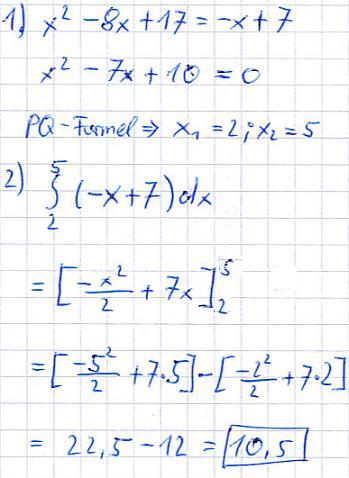
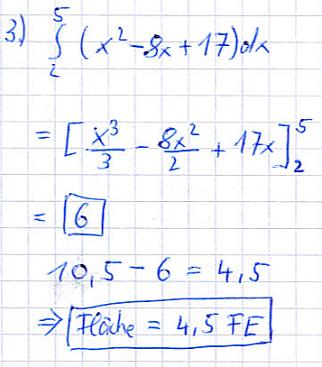
Noch einmal zum Nachvollziehen:

• Um die Integrationsgrenzen zu erhalten, haben wir die beiden Schnittpunkte der Funktionsgraphen berechnet
• Wir haben innerhalb dieser Grenze die Fläche unter g(x) berechnet
• Wir haben innerhalb dieser Grenze die Fläche unter h(x) berechnet
• Die Differenz ist die gesuchte, grün eingezeichnete Fläche

Es folgen einige weitere Beispiele, welche die Berechnung von Flächen zwischen Kurven zeigen. Um den Artikel nicht extrem in die Länge zu ziehen, wird bei diesen jedoch nur auf den allgemeinen Lösungsweg eingegangen.

Beispiel 2 zur Flächenberechnung:

Kommen wir zu einem weiteren Beispiel, an dem die prinzipielle Denkweise verdeutlicht werden soll:

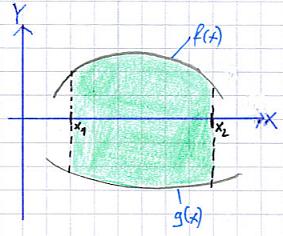
Zur Berechnung der Fläche müsste man nun wie folgt vorgehen:

• Die Funktionsgraphen haben keine Schnittpunkte, sondern werden in unserem Beispiel von x₁ und x₂ begrenzt.
• Die Fläche unter f(x) in den Grenzen wird berechnet. Dazu wird das Integral in den Grenzen x₁ und x₂ wie gewohnt für f(x) berechnet
• Die Fläche über g(x) wird berechnet. Dazu wird das Integral in den Grenzen x₁ und x₂ wie gewohnt für g(x) berechnet. Rechnerisch erhält man eine negative Fläche. Man nimmt von diesem Wert jedoch den Betrag.
• Die Fläche unter f(x) und der Betrag der Fläche unter g(x) in den Grenzen x₁ und x₂ werden addiert und bilden den gesamten Flächeninhalt.

Beispiel 3:

Unser nächstes Beispiel wird noch ein Stück komplizierter. Auch hier erst einmal eine Grafik. Seht euch diese gründlich an:

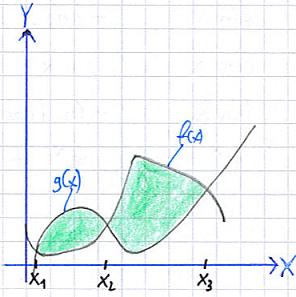
Zur Berechnung der Fläche müsste man wie folgt vorgehen:

• Die Funktionen f(x) und g(x) schneiden sich in diesem Beispiel drei mal. Die Schnittpunkte müssen wie in Beispiel 1 berechnet werden
• Die linke grüne Fläche berechnet sich ähnlich wie in Beispiel 1: Die Flächen unter f(x) und g(x) werden in den Grenzen x₁ und x₂ jeweils berechnet. Die Differenz der Flächen ist die linke, grüne Fläche.
• Die rechte grüne Fläche berechnet sich ähnlich wie in Beispiel 1: Die Flächen unter f(x) und g(x) werden in den Grenzen x₂ und x₃ jeweils berechnet. Die Differenz der Fläche ist die rechte, grüne Fläche.

Links:

• Zur Integral-Übersicht
• Zur Mathematik-Übersicht