Aufleiten Substitution ( Aufleitung )

Mit dem Aufleiten durch Substitution befassen wir uns in diesem Artikel. Dabei wird erklärt, warum man die  Aufleitung durch Substitution benötigt und es werden Beispiele vorgerechnet. Dieser Artikel gehört zu unserem Bereich Mathematik.

Zunächst ein wichtiger Hinweis: Der Begriff "Aufleiten" ist umgangssprachlich. Er wird von vielen Schülern einfach als das Gegenteil von Ableiten angesehen. In der Mathematik spricht man bei diesem Bereich richtigerweise von Integration bzw. von Integrationsregeln. Dieser Artikel hier richtet sich also mehr an Schüler bzw. Studenten, die sich der Sache von der Umgangssprache her genähert haben.

Aufleiten durch Substitution Vorgehensweise

Klären wir zunächst, was man unter einer Substitution überhaupt versteht: Unter Substitution versteht man allgemein das Ersetzen eines Terms durch einen anderen. Und genau das tun wir nun um eine Integration durchzuführen. Ich zeige dies gleich durch das Vorrechnen einiger Beispiele. Zunächst jedoch die allgemeine Vorgehensweise:

1. Substitution, Ableitung und Umstellen
2. Substitution bei der Integralaufgabe durchführen
3. Integral lösen
4. Rücksubstitution durchführen

Aufleiten durch Substitution

Anhand der eben genannten Punkte sollen nun einige Beispiele zur Aufleitung durch Substitution vorgerechnet werden. Denn Beispiele verdeutlichen die Vorgehensweise oft am besten.

Aufleiten Beispiel 1: Im ersten Beispiel soll ein Bruch aufgeleitet werden. Dabei halten wir uns an den 4-Punkte-Plan weiter oben. Im Schritt 1 substituieren wir den Nenner. Im Anschluss leiten wir ab und stellen nach dx um.  In Schritt 2.) setzen wir für 5x - 7 nun z ein und für dx setzen wir dz durch 5 ein. In Schritt Nr. 3 geht es dann darum die Aufleitung durchzuführen. Und im letzten Schritt führen wir die Rücksubstitution durch.

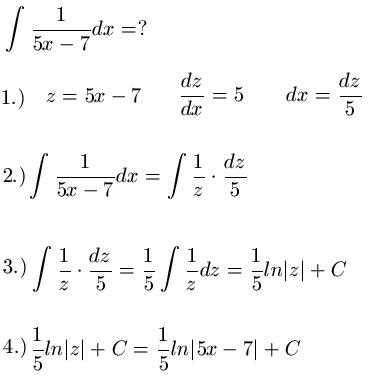
Aufleiten Beispiel 2: Im zweiten Beispiel zur Aufleitung durch Substitution geht es darum eine Sinus-Funktion zu integrieren. Die Vorgehensweise sieht dabei aus wie im ersten Beispiel: Wir führen in Schritt 1.) zunächst eine Substitution durch, leiten ab und stellen nach dx um. Im Schritt 2.) setzen wir für 3 - 7x nun z ein und für dx nun dz durch -7. Im dritten Schritt geht es nun darum das Integral zu lösen um im letzten Schritt wird die Rücksubstitution durchgezogen.

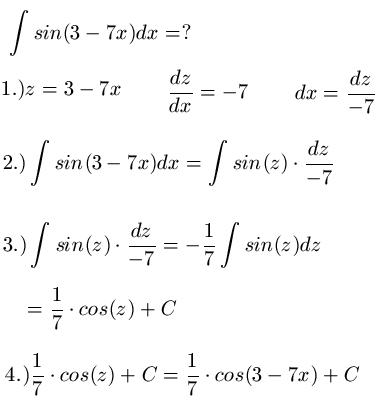
Aufleiten Beispiel 3: Im Beispiel Nr. 3 soll nun eine Fläche berechnet werden. Auch hier geht es zunächst erst einmal darum das Integral durch Einsatz von Substitution zu lösen, also die Aufleitung durchzuführen. Nach der Rücksubstitution in Schritt 4.) geht es im Schritt 5.) dann um die Berechnung der Fläche. Also die obere und untere Grenze jeweils einsetzen, ausrechnen und die Differenz bilden. So wie man das bei der Flächenberechnung mit Integralen eben macht.

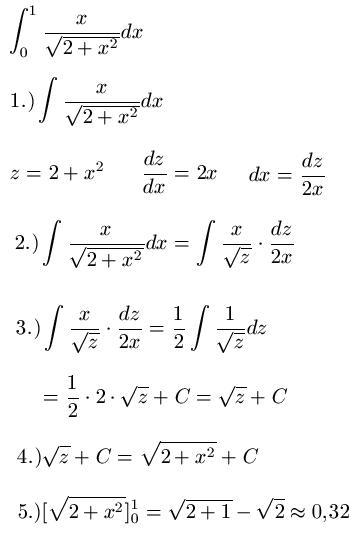
Links:

• Aufgaben / Übungen zu Aufleiten durch Substitution
• Zur Integrations-Übersicht
• Zur Mathematik-Übersicht