Mit der bedingten Wahrscheinlichkeit befassen wir uns in diesem Artikel. Dabei erklären wir euch, was man unter der bedingten Wahrscheinlichkeit überhaupt versteht und liefern euch ein Beispiel für die Berechnung. Dieser Artikel gehört zum Bereich Mathematik / Stochastik.
Vieles im Leben hängt von früheren Ereignissen ab. Beispiel: Ihr habt sehr gut für ein Fußball-Turnier trainiert. Dadurch steigen nun beim Turnier eure Chancen, dieses zu gewinnen. Solche Abhängigkeiten gibt es auch in der Mathematik und werden als "Bedingte Wahrscheinlichkeit" bezeichnet. An einem etwas ausführlicherem Beispiel möchten wir euch nun die bedingte Wahrscheinlichkeit näher erläutern.
Beispiel:
In der Medizin ist es seit längerem möglich, Menschen auf HIV zu testen. So ein Test ist jedoch nicht zu 100% zuverlässig. So kann es leider passieren, dass der Test das Ergebnis "HIV positiv" anzeigt, obwohl der Mensch kein HIV hat. Und umgekehrt kann ein HIV infizierter Mensch fälschlicherweise als nicht HIV-infiziert getestet werden.
Die Tests sind in Zwischenzeit jedoch recht zuverlässig geworden: Bei 99,9% der tatsächlich Infizierten erfolgt eine positive Testreaktion. Nur bei 0,3% der nichtinfizierten Testpersonen wird fälschlich eine Infektion angezeigt. Es wird angenommen, dass 0,1 Prozent der Bevölkerung HIV-infiziert ist.
Aufgabe: Zunächst soll eine Vierfeldertafel für die Aufgabe erstellt werden. Im Anschluss soll ein Baumdiagramm erstellt werden.
Lösung: Dem Text entnehmen wir die entsprechenden Prozentangaben und erstellen mit diesen unsere Vierfeldertafel:
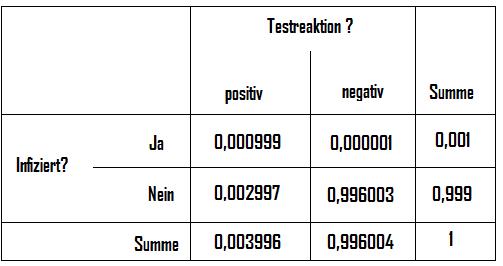
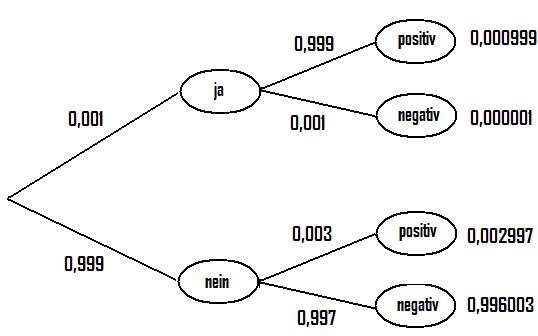
Für das Baumdiagramm wählen wir in der 1. Stufe das Vorliegen der Infektion bzw. in der 2. Stufe die Testreaktion. Aus diesem sehen wir, dass die Testreaktion vom vorliegen einer Infektion abhängig ist. Wir haben somit eine bedingte Wahrscheinlichkeit.
Links:
174 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
