Bogenmaß und Gradmaß + Umrechnung

Mit dem Bogenmaß und Gradmaß und auch deren Umrechnung befassen wir uns in diesem Artikel. Letzteres wird vor allem durch das Vorrechnen einiger Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

In diesem Artikel geht es um das Gradmaß und das Bogenmaß sowie die Umrechnung zwischen diesen beiden. Zu Beginn klären wir jedoch erst einmal, was man unter dem Gradmaß und auch unter dem Bogenmaß überhaupt versteht und gehen erst im Anschluss auf die Umrechnung ein.

Gradmaß:

In der Schule lernt man normalerweise zunächst das Gradmaß kennen. Dabei entspricht eine komplette Umrundung eines Kreises 360 Grad. Steht also eine Person in einem Raum und dreht sich einmal um sich herum, so dass sie wieder in die gleiche Richtung blickt wie vor der Drehung, dann wurden dabei 360 Grad überschritten.  Ein weiteres Beispiel: Wir haben zwei Geraden und zwischen diesen bildet sich ein Winkel aus. Dieser wird in der folgenden Grafik als α ( gesprochen Alpha ) bezeichnet und ist so in etwa 40 Grad.

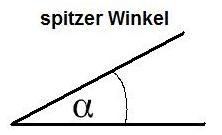
Bogenmaß:

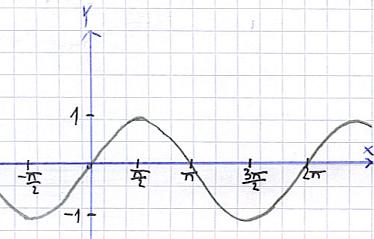
In der Mathematik, vor allem aber auch in der Physik ist das Bogenmaß von Interesse. Ein oft verwendetes Beispiel dafür ist eine Schwingung, zum Beispiel der Sinus. Wird ein Sinusverlauf komplett vollzogen, so hat man ebenfalls 360 Grad durchlaufen, oder im Bogenmaß ausgedrückt 2π. Die folgende Grafik zeigt den Verlauf eines Sinus.

Bogenmaß und Gradmaß umrechnen / umwandeln

Wie im letzten Abschnitt bereits angedeutet, entsprechen 360 Grad im Gradmaß 2π im Bogenmaß. Damit haben wir eigentlich schon eine Möglichkeit gefunden, diese beiden Angaben ineinander umzurechnen. Die Formeln dafür lauten:

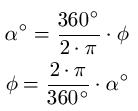
Beispiele:

Das Gradmaß 23° soll ins Bogenmaß umgerechnet werden.

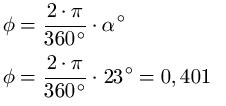
Das Bogenmaß 0,6 rad soll ins Gradmaß umgewandelt werden.

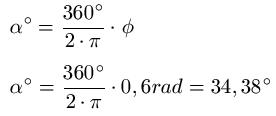
Links:

• Zur Mathematik-Übersicht