Mit Bruchgleichungen befassen wir uns in diesem Artikel. Dabei erklären wir euch, was eine Bruchgleichung ist und wie man diese löst. Dieser Artikel gehört zum Bereich Mathematik.
Bevor wir mit den Bruchgleichungen starten, solltet ihr eure Vorkenntnisse kurz überprüfen. Sind eure Kenntnisse im Bereich der Bruchrechnung oder bei den Gleichungen noch sehr schwach, so lest zunächst die beiden nun verlinkten Artikel. Alle anderen können gleich mit den Bruchgleichungen starten:
Bruchgleichungen lösen
Bevor wir mit Rechnungen beginnen, sollten zwei wichtige Dinge geklärt werden. 1. Was ist ein Bruchterm und 2. Was ist eine Bruchgleichung? Unter einem Bruchterm versteht man einen Bruch, dessen Nenner - das ist die Zahl unter dem Bruchstrich - eine Variable enthält. Und eine Bruchgleichung ist eine Gleichung, die mindestens einen Bruchterm enthält.
Bruchgleichungen lassen sich wie auch lineare Gleichungen durch Äquivalenzumformungen lösen. Zuvor muss jedoch ein Blick auf die Nenner der Bruchgleichungen geworfen werden, um die Definitionsmenge zu bestimmen. Es gilt: Es darf kein Wert für eine Variable eingesetzt werden, welcher zu einer Division durch Null führt. Zu bestimmen sind also die Nennernullstellen, denn genau diese Werte gehören nicht zur Definitionsmenge.
Bruchgleichungen Beispiele
In aller Regel bringt es Schülern beim Verständnis zu Bruchgleichungen am meisten, wenn sie passende Beispiele vorgerechnet bekommen. Dies möchten wir im nun Folgenden tun. Dabei zeigen wir zunächst ein Rechenbeispiel und erläutern im Anschluss den Rechenweg in Textform.
Beispiel 1:
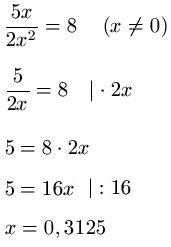
Für die Bruchgleichung bestimmen wir die Definitionsmenge: Der Nenner würde 0 werden, wenn wir für x = 0 einsetzen würden. Da Zähler und Nenner nur aus Produkten bestehen und beide ein "x" enthalten, kürzen wir dieses. Anschließend multiplizieren wir mit 2x und lösen anschließend nach x auf.
Beispiel 2:
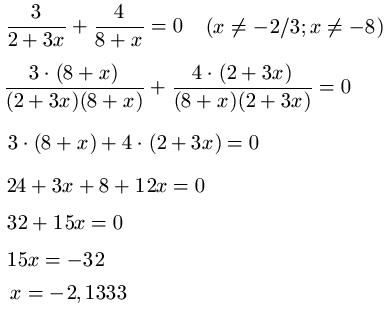
Auch hier untersuchen wir die Bruchgleichung im Hinblick auf die Definitionsmenge. Dabei zeigt sich, dass x = -8 und x =-2/3 nicht eingesetzt werden dürfen. Im Anschluss nutzen wir den Hauptnenner. Dieser lautet ( 2 + 3x ) ( 8 + x ). Als Letztes wird die Gleichung nach x aufgelöst.
Links:
180 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
