Brüche vergleichen und ordnen

Wie man Brüche vergleicht und ordnet, erklären wir euch hier. Dabei zeigen wir euch, was gleichnamige und ungleichnamige Brüche sind und wie man Brüche umwandelt. Einige Beispiele verdeutlichen dies.

Welcher Bruch ist größer? Welcher Bruch ist kleiner? Diese Frage taucht immer mal wieder in der Bruchrechnung auf. Ein Bruch dient dazu, Anteile an etwas Ganzem darzustellen. Damit es keine Verwirrung bei den Begriffen gibt, noch eine schnelle Grafik:

Sind die Nenner bei allen Brüchen gleich, bezeichnet man diese als gleichnamige Brüche. Sind die Nenner der Brüche verschieden, bezeichnet man diese als ungleichnamige Brüche.

Beim Vergleichen von Brüchen unterscheidet man drei unterschiedliche Fälle.

1. Die Nenner der Brüche sind alle gleich.
2. Die Zähler der Brüche sind alle gleich.
3. Zähler und Nenner sind verschieden.

Beispiele Brüche vergleichen

Sehen wir uns Beispiele zu diesen drei Fällen an.

Beispiel 1:
Diese drei Brüche sollen der Größe nach geordnet werden, beginnend mit dem größten Bruch.

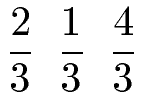
Lösung:
Die drei Brüche sind gleichnamig, denn der Nenner ist immer 3. Das Vergleichen der Brüche wird dadurch sehr einfach. Je größer der Zähler, desto größer der Bruch. Das Zeichen für Größer ist das ">".

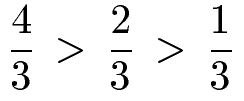
Beispiel 2:
Erneut haben wir drei Brüche. Die Brüche sollen sortiert werden, die kleinste Zahl soll ganz links stehen.

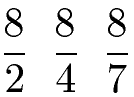
Lösung:
Die drei Nenner sind verschieden, daher haben wir hier ungleichnamige Brüche. Die Zähler sind hingegen gleich. Dies machen wir uns beim Vergleichen der Brüche zunutze. Je größer der Nenner ist, desto kleiner ist der Bruch. Würde man den Bruch in eine Dezimalzahl wandeln, sieht man dies auch:

• 8 : 7 = 1,1429
• 8 : 4 = 2
• 8 : 2 = 4

Daher ist 8 : 7 der kleinste Bruch und 8 : 2 der größte Bruch. Das Sortieren der Brüche sieht damit so aus:

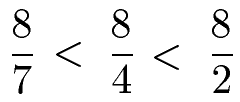
Beispiel 3:
Die nächsten drei Brüche sollen verglichen und geordnet werden.

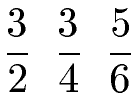
Lösung:
Wir suchen zunächst einen gemeinsamen Nenner für alle Brüche. Um diesen zu finden, verwenden wir das kleinste gemeinsame Vielfache. Dazu nehmen wir die Nenner 2, 4, 6 und schreiben jeweils deren Vielfache auf. Dann suchen wir die kleinste gemeine Zahl darunter, welches die 12 ist.

2: 2, 4, 6, 8, 10, 12, 14
4: 4, 8, 12, 16, 20, 24
6: 6, 12, 18, 24, 30, 36

Der gemeinsame Nenner wäre damit 12. Als nächstes müssen wir die Zähler genauso anpassen. Um bei 3 : 2 auf 12 im Nenner zu kommen, muss man mit 6 multiplizieren. Dies machen wir auch im Zähler und erhalten 3 · 6 = 18. Der zweite Bruch lautete 3 : 4. Um hier auf 12 im Nenner zu kommen, muss mit 3 multipliziert werden. Dies machen wir auch im Zähler: 3 · 3 = 9. Fehlt mit 5 : 6 noch der letzte Bruch. Hier muss der Nenner mit 2 multipliziert werden, um auf 12 zu kommen. Dies machen wir auch im Zähler: 5 · 2 = 10.

Die drei Brüche sind damit:

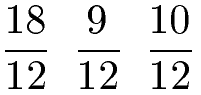
Die Brüche sind nun gleichnamig und wir können mit einem Blick auf den Zähler diese ordnen:

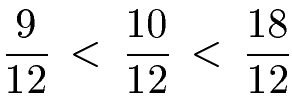
Wir erhalten damit:

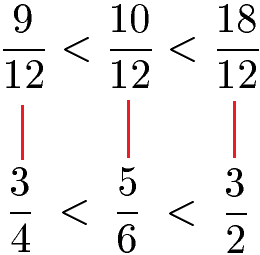
Links:

• Zur Mathematik-Übersicht