Erwartungswert

Mit dem Erwartungswert befassen wir uns in diesem Artikel. Dabei geben wir euch nicht nur die allgemein Formel zur Berechnung des Erwartungswerts, sondern auch Beispiele zum besseren Verständnis an. Dieser Artikel gehört zum Bereich Mathematik.

Führt man einen Zufallsversuch sehr oft durch und bildet aus den Ergebnissen den ( gewichteten ) Mittelwert, so erhält man den Erwartungswert. Es folgt nun erst einmal die allgemeine Darstellung, die im Anschluss folgenden Beispiele dürften beim Verständnis jedoch deutlich mehr helfen.

Der Erwartungswert

X sei eine endliche Zufallsgröße, welche genau die Werte X_i annehmen kann. Dabei hat dieser jeweils die Wahrscheinlichkeit P ( X = x_i ). Dann berechnet sich die Erwartungswert nach der Formel:

• E(X) = x₁ · P(X = X₁ ) + x₂ · P(X = x₂ ) + ... + X_n · P(X = X_n )

Beispiel 1:

Wir haben eine Grafik, in der die Wahrscheinlichkeit für eine bestimmte Anzahl eingetragen wird. Ziel ist es, für diese Angaben den Erwartungswert zu berechnen.

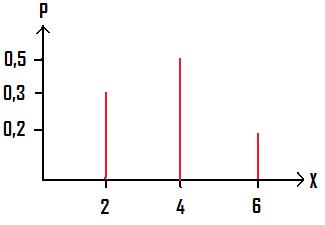
Lösung: E(X) = 2 · 0,3 + 4 · 0,5 + 6 · 0,2 = 3,8

Beispiel 2:

Wir untersuchen im nun Folgenden einen Spielautomat. Der Einsatz pro Spiel kostet 1 Euro. Eine Tabelle informiert, wie groß die Wahrscheinlichkeit für einen ausgezahlten Betrag in Euro ist. Die Frage lautet: Wie groß ist der durchschnittliche Gewinn ( Erwartungswert )?

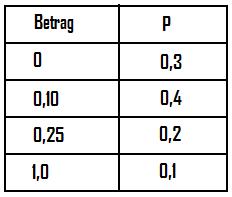
Lösung: E(X) = 0 · 0,3 + 0,10 · 0,4 + 0,25 · 0,2 + 1,0 · 0,1 = 0,19

Im Durchschnitt spuckt der Automat somit pro Spiel 0,19 Euro aus. Ein Spiel kostet 1 Euro. Somit verdient der Automatenbetreiber 81 Cent pro Spiel. Das Spiel ist totale Abzocke, denn der eingesetzte Einsatz ist so hoch wie der maximal auszahlbare Betrag.

Links:

• Zur Stochastik-Übersicht
• Zurück zur Mathematik-Übersicht