Wie kann man Gleichungen lösen? Genau dazu liefert dieser Artikel Erklärungen, Beispiele und Aufgaben. Wie sehen uns dazu einfache lineare Gleichungen , quadratische Gleichungen und Funktionen höheren Grades an. Gleichungssysteme kann man mit Gauß-Verfahren oder auch Einsetzungsverfahren bzw. Additionsverfahren lösen. Insgesamt geht es darum mit Umformungen die Lösungsmenge zu finden. Dieser Artikel gehört zu unserem Bereich Mathematik.
Wie kann man eine Gleichung lösen? Nun, dies hängt von der Art der Gleichung ab. Und aus genau diesem Grund müssen wir uns hier logischerweise auch mit verschiedenen Arten von Gleichungen befassen. Wie beginnen dabei mit dem Lösen von linearen Gleichungen.
Gleichungen lösen bzw. auflösen: Lineare Gleichung
Das Lösen von linearen Gleichungen hat schon viele Schüler und Schülerinnen zur Verzweiflung getrieben. Fangen wir daher lieber einmal ganz einfach an. Deshalb beginnen wir mit etwas, dass jeder schon aus der Grundschule kennen müsste, einer Gleichung. Kein Witz!
- 3 + 4 = 7
Das ist eine ganz einfache Gleichung. Denn links erhalten wir 7 und rechts erhalten wir 7. Also 7 = 7 erhalten wir, eine wahre Aussage. Dies trifft auch auf das Lösen von linearen Gleichungen zu. Was nun neu ist, dass noch eine Variable in der Gleichung auftaucht. Was ist eine Variable? Eine Variable ist sozusagen ein "Platzhalter" für eine Zahl. Zumindest ist es in den allermeisten Fällen eine Zahl. In der Mathematik wird in der Regel ein Buchstabe dafür eingesetzt. Das ist dann z.B. ein a, b, x oder y. Anstelle dieser Variable wird später eine Zahl eingesetzt. Das Ziel ist es, herauszufinden, wie groß die Zahl der Variable ist. Und genau damit beschäftigen wir uns in den folgenden Abschnitten.
Wie schon in der Einleitung erklärt, soll nun eine lineare Gleichung mit einer Unbekannten gelöst werden. Diese Unbekannte wird im Unterricht meistens "x" genannt, andere Buchstaben (Variablen) sind auch möglich. Ziel ist es, dass am Ende "x = eine Zahl" als Lösung angegeben werden kann. Los geht es mit einer ganz einfachen Aufgabe. Diese wird anschließend erklärt.
Tabelle nach rechts scrollbar
| Beispiel 1: | |
| x + 2 = 5 | | -2 |
| x = 3 |
In der ersten Zeile findet sich die Ausgangsgleichung, welche nach der Variablen x aufgelöst werden soll. Um dies durchzuführen, müssen sogenannte Äquivalenzumformungen oder manchmal einfach Umformungen durchgeführt werden. Dies bedeutet: Das Aussehen der Gleichung wird verändert, aber dennoch steht auf der linken Seite der selbe Wert wir auf der rechten Seite der Gleichung. Um nun nach "x" aufzulösen, muss die 2 auf der linken Seite "beseitigt" werden. Um eine +2 zu entfernen, muss mit "-2" gerechnet werden. Zur besseren Übersicht werden alle Rechenoperationen hinter ein "|" geschrieben. So wird nun "| -2" aufgeschrieben, um klar zu erkennen, dass eine 2 abgezogen werden soll. Ganz, ganz wichtig: Rechenoperationen müssen auf beiden Seiten durchgeführt werden. Rechne ich auf der linken Seite "-2", muss dies auch rechts getan werden!
Tabelle nach rechts scrollbar
| Beispiel 2: | |
| x - 5 = 2 |
| + 5 |
| x = 7 |
Tabelle nach rechts scrollbar
| Beispiel 3: | |
| 4 = x + 2 | | -2 |
| 2 = x |
Tabelle nach rechts scrollbar
| Beispiel 4: | |
| 4 - 3 + x = 5 - 2 | |
| 1 + x = 3 | | -1 |
| x = 2 |
Soweit erst einmal zur Addition und Subtraktion bei Gleichungen. An Beispiel 4 sieht man gut, dass es oftmals erst einmal sinnvoll ist, die Gleichung zu vereinfachen, bevor Umformungen durchgeführt werden.
Multiplikation und Division:
Bisher musstet ihr um eine "+2" zu beseitigen mit "-2" rechnen und eben auch umgekehrt. Dies gilt auch für Multiplikation und Division, um eben entsprechende Gleichungen zu lösen. Um eine "·5" zu entfernen, müsst ihr ":5" berechnen. Klingt erstmal etwas seltsam, die folgende Aufgabe zeigt euch jedoch, wie dies funktioniert. Auch hier soll nach "x" aufgelöst werden.
Tabelle nach rechts scrollbar
| Beispiel 5: | |
| 5 · x = 15 | | :5 |
| x = 3 |
Damit "x" alleine steht, muss durch 5 geteilt werden. Denn: 5 : 5 = 1 und 1 · x = x. Wem das zu kompliziert ist, der muss sich einfach nur merken: Um 5 · x weg zu bekommen, muss ich durch 5 teilen. Anmerkung: Die Schreibweise 5 · x entspricht mathematisch gesehen 5x. Steht kein Rechenzeichen zwischen Zahl und Variable, wird eine Multiplikation durchgeführt. So auch bei den nächsten Aufgaben.
Tabelle nach rechts scrollbar
| Beispiel 6: | |
|
0,5x = 2 |
| :0,5 |
| x = 4 |
Tabelle nach rechts scrollbar
| Beispiel 7: | |
| 5 = 0,2x | | :0,2 |
| 25 = x |
Machen wir das Ganze mal etwas schwieriger. Bei den nächsten Aufgaben wird es nötig sein, dass ihr die Punkt vor Strich und Klammerrechnung beachtet. Ansonsten werden die Ergebnisse (normalerweise) falsch sein. Fangen wir wie immer mit einem Beispiel an.
Tabelle nach rechts scrollbar
| Beispiel 8 | |
| 5 · 8 + x = 10 | |
| 40 + x = 10 | | -40 |
| x = -30 |
Auch hier gilt: Punktrechnung vor Strichrechnung. Multiplikationen und Division werden zuerst berechnet, danach Addition und Subtraktion. Und gleich noch zwei weitere Aufgaben:
Tabelle nach rechts scrollbar
| Beispiel 9: | |
| 40 + 20x = 20 | | :20 |
| 2 + x = 1 | | -2 |
| x = -1 |
Tabelle nach rechts scrollbar
| Beispiel 10: | |
| 3 + 5 · 2 + 5x = 10 | |
| 3 + 10 + 5x = 10 | |
| 13 + 5x = 10 | | -13 |
| 5x = -3 | | :5 |
| x = -0,6 |
Gleichungen lösen bzw. auflösen: Quadratische Gleichungen
Wir hatten uns eben mit dem Lösen oder auch Auflösen von linearen Gleichungen befasst. Gehen wir nun zum Lösen von quadratischen Gleichungen. Da stellt sich natürlich die Frage: Was ist eine quadratische Gleichung? Nun, dabei handelt es sich um eine Gleichung mit der Form ax2 + bx + c = 0 oder eine Gleichung die man auf diese Form mit Umwandlungen bringen kann. Die Variablen a, b und c stehen für irgendwelche Zahlen, wobei a ungleich Null sein muss. Es folgen zwei Beispiele bzw. Aufgaben: 3x2 + 5x + 3 = 0 oder auch x2 + 2x + 1 = 0.
Im Gegensatz zu "einfachen" Gleichungen, die wir bisher kennen gelernt hatten (Beispiel: x + 5 = 0) ist hier noch ein quadratischer Anteil vorhanden. Wie also löst man nun diese Gleichung nach x auf? Die Antwort auf diese Frage lautet PQ-Formel, mit der wir uns in diesem Abschnitt beschäftigen möchten. Hinweis: Es gibt neben der PQ-Formel noch andere Möglichkeiten eine quadratische Gleichung zu lösen (Mitternachtsformel bzw. ABC-Formel oder auch Polynomdivision). Wir möchten hier in diesem umfassenden Artikel zum Gleichungen lösen jedoch nur eine Variante ausführlich vorstellen und haben uns für die PQ-Formel entschieden.
Quadratische Gleichung lösen: Lösungsformel
Wie kann man nun so eine Gleichung lösen? Um eine Gleichung wie z.B. x2 + 2x + 1 = 0 nach x aufzulösen, setzen wir im nun Folgenden die PQ-Formel ein. Ich gebe euch nun erst einmal die Formel an sowie ein paar allgemeine Informationen. Keine Panik: Einige Aufgaben erläutern dies im Anschluss.
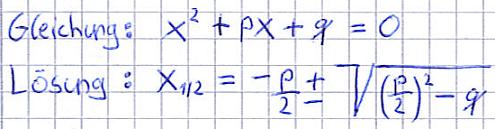
Quadratische Gleichung lösen:
- Bringt die Gleichung in die Form x2 + px + q = 0
- Findet "p" und "q" raus
- Setzt dies in die PQ-Formel ein
- Berechnet die Lösung damit
Soviel zum Plan. Zeit dies Anhand von ein paar Aufgaben zu klären. Verfolgt diese Beispiele anhand der 4-Punkte-Liste von eben.
Wichtiger Hinweis: Um Schüler nicht gleich mit vielen Brüchen zu verwirren wurde bei einigen Beispielen gerundet.
Beispiel 1:
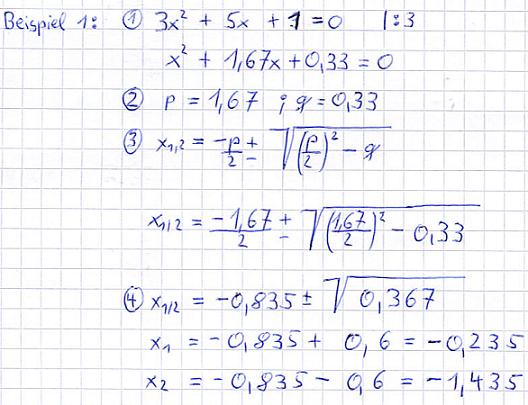
Erläuterungen: Die "3" vor dem x2 stört! Dort muss immer eine "1" stehen, sprich 1x2. Um dies zu erreichen, wird durch 3 geteilt. Danach werden p und q abgelesen. Die Zahlen von p und q werden in die Lösungsformel eingesetzt. Danach wird der Ausdruck vor und unter der Wurzel berechnet. Anschließend wird die Wurzel aus dem Wert gezogen und es wird einmal addiert und einmal subtrahiert. Eine quadratische Gleichung hat maximal zwei Lösungen im reellen. Also in der Schule hat eine quadratische Gleichung maximal zwei Lösungen, im Studium immer zwei Lösungen (sofern man komplexe Zahlen erlaubt, aber die behandeln wir hier nicht).
Beispiel 2:
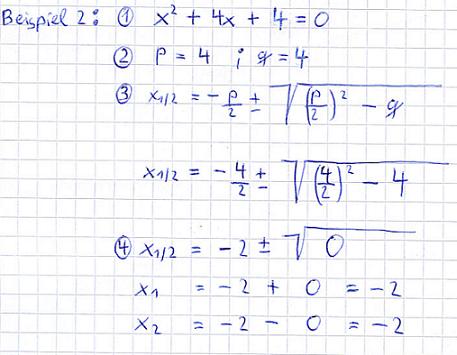
Erklärungen: Die ursprüngliche Aufgabe ist bereits in der richtigen Form. Deshalb kann p und q gleich bestimmt werden. Diese dann in die Gleichung einsetzen und ausrechnen. Wie ihr am Ergebnis seht, gibt es die Lösung -2 doppelt, sprich x1 = -2 und x2 = -2.
Gleichungen lösen bei negativer Wurzel
Es gibt noch zwei kleine Hinweise beim Lösen von quadratischen Gleichungen bzw. quadratischen Funktionen mit der PQ-Formel von uns:
- Wenn ihr die Zahlen unter der Wurzel berechnet und dann eine negative Zahl unter der Wurzel steht, dürft ihr abbrechen. Dann hat die Gleichung keine Lösung (zumindest nicht für Schüler, Studenten müssen dann mit imaginären Rechnen).
- Achtet auf das Vorzeichen! Habt ihr zum Beispiel die Aufgabe x2 -5x + 3 = 0 zu lösen, dann ist p = -5. Diese -5 müsst ihr dann auch in der PQ-Formel einsetzen!
Für beide Fälle findet ihr hier noch jeweils ein Beispiel:
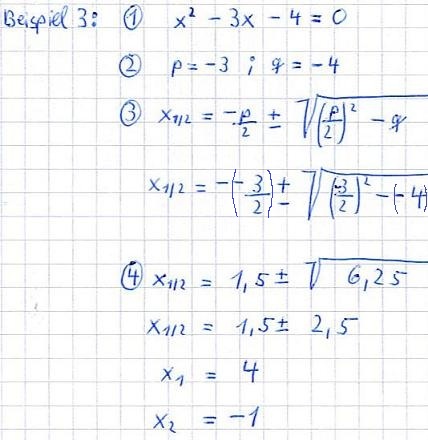
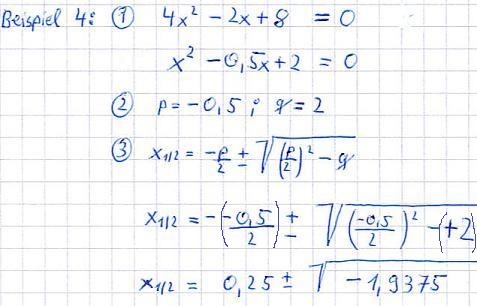
Gleichungen lösen : ABC - Formel oder Mitternachtsformel
Das Lösen von Gleichungen - besser gesagt quadratischen Gleichungen - kann man auch mit der ABC-Formel bzw. Mitternachtsformel durchführen. Die ABC - Formel ähnelt sehr stark der PQ-Formel und dient der Lösung quadratischer Gleichungen. Sofern man richtig rechnet, kommt man mit beiden Formeln auf das gleiche Ergebnis. Es folgen nun die allgemeine Formel samt Lösung und im Anschluss wenden wir uns einem Beispiel zu.
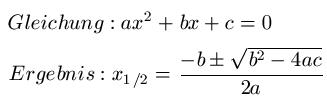
Mehr zu dieser Lösungsmethode im Artikel ABC-Formel.
Gleichungen lösen: 3. Potenz und höher
Die Polynomdivision ist ein Verfahren der Mathematik, um Nullstellen von Polynomen zu berechnen. Man kann damit auch Gleichungen höheren Grades lösen. Die Berechnungsweise ähnelt der schriftlichen Division, die man bereits in der Grundschule kennengelernt hat. Aus diesem Grund gehen wir im nun Folgenden erst einmal kurz auf die schriftliche Division ein und wenden dieses Wissen dann auf die Polynomdivision an.
Um den Artikel hier nicht noch länger werden zu lassen, gibt es alles weitere zur Polynomdivision im entsprechenden Artikel: Polynomdivision.
Lineare Gleichungssysteme lösen
Sehen wir uns das Gleichungen lösen einmal auf eine andere Art und Weise an. Zunächst einmal solltet ihr Wissen, was man unter einem Gleichungssystem mit zwei Variablen überhaupt versteht. Dazu erst einmal ein kleines Beispiel: Ihr geht einkaufen und wisst, dass 6 Äpfel und 12 Birnen besonders guter Qualität 30 Euro kosten. Und ihr wisst, dass 3 Äpfel und 3 Birnen 9 Euro kosten. Die Frage lautet nun: Was kostet ein Apfel oder eine Birne? Da die Begriffe Äpfel und Birnen zu lange sind, setzen wir für den Preis für einen Apfel "x" und für den Preis einer Birne "y" ein. Daraus entstehen die folgenden Gleichungen ( Vergleicht diese mit den Angaben im Text! ):
Tabelle nach rechts scrollbar
| 6 | Äpfel | und | 12 | Birnen | kosten | 30 Euro |
| 6 | x | + | 12 | y | = | 30 |
| 3 | Äpfel | und | 3 | Birnen | kosten | 9 Euro |
| 3 | x | + | 3 | y | = | 9 |
Das sieht natürlich noch nicht so sonderlich übersichtlich aus. Aus diesem Grund hat man in der Mathematik die folgende Schreibweise eingeführt, um für mehr Übersicht zu sorgen:
Tabelle nach rechts scrollbar
| | 6x + 12y | = | 30 | | Gleichung Nr. 1 |
| | 3x + 3y | = | 9 | | Gleichung Nr. 2 |
Ein solches Gleichungssystem deutet an: Diese Gleichungen gehören zu einander. Dies ist auch der Grund, warum man sie gemeinsam lösen muss. Ziel ist es, für x und y eine Zahl zu erhalten, die beide Gleichungen erfüllt. Und darum kümmern wir uns jetzt.
Um den Artikel nicht noch länger werden zu lassen, gibt es alles Weitere zu linearen Gleichungssystemen in unserem Artikel lineare Gleichungssysteme.
Weiterführende Artikel:
- ABC-Formel: Mit der ABC-Formel bzw. Mitternachtsformel kann man ebenfalls quadratische Gleichungen lösen. Wie dies funktioniert, lernt ihr in unserem Artikel ABC-Formel.
- Polynomdivision: Die Polynomdivision ist ein Verfahren zum Auffinden von Nullstellen bei Gleichungen mit höherer Potenz. Wie dies funktioniert und wie man damit auch Gleichungen lösen kann, lernt ihr im Artikel Polynomdivision.
- Nullstellen: Wie findet man Nullstellen? Einen ausführlichen Artikel mit verschiedenen Verfahren, Beispielen und Aufgaben findet ihr im Artikel Nullstellen berechnen.
Weitere Links:
217 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: