Was das halbschriftliche Rechnen ist und wofür man es braucht, zeige ich dir in diesem Artikel. Dies umfasst die halbschriftliche Addition, Subtraktion, Multiplikation und auch Division. Beispiele mit Erklärungen dazu bekommst du ebenfalls.
Werden die Zahlen etwas größer fällt es vielen Schülern und Schülerinnen schwerer Aufgaben zu berechnen. Aus diesem Grund hilft man sich mit anderen Rechenmethoden weiter. Eine Möglichkeit besteht im halbschriftlichen Rechnen, welches ab der 2. Klasse in der Grundschule behandelt wird. Diese Rechenmethode gibt es für alle vier Grundrechenarten, sprich für Addition, Subtraktion, Multiplikation und Division.
Halbschriftliche Addition:
Bei der halbschriftlichen Addition (auch halbschriftlich plus genannt) zerlegt man die Rechenaufgabe um einfacher Addieren zu können.
Beispiel 1: Halbschriftliche Addition
Im nächsten Beispiel ist dies 35 + 42. Zunächst rechnen wir 35 + 40 und auf das Ergebnis noch einmal +2 drauf. Die zweite Zahl wird damit in Einer (2) und Zehner (40) zerlegt und einzeln gerechnet.
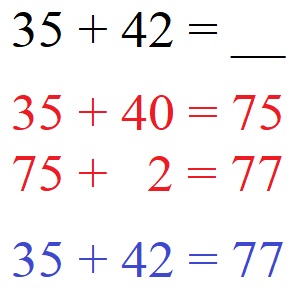
Beispiel 2: Halbschriftliche Addition
Im zweiten Beispiel werden dreistelligen Zahlen halbschriftlich addiert. Die 214 wird in 200, 10 und 4 zerlegt und einzeln addiert.
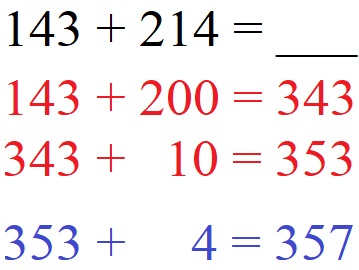
Man nennt dies auch ein Zerlegen der Zahl in Hunderter, Zehner und Einer. Die halbschriftliche Addition wird meistens im Zahlenraum bis 1000 verwendet. Werden die Zahlen noch größer wird die schriftliche Addition eingesetzt.
Halbschriftliche Subtraktion
Bei der halbschriftlichen Subtraktion wird ebenfalls die zweite Zahl in Einer, Zehner, Hunderter und so weiter zerlegt.
Beispiel 3: Halbschriftliche Subtraktion
Berechnet werden soll 65 - 23. Dazu rechnen wir erst einmal 65 minus 20 und ziehen vom Ergebnis noch einmal 3 ab.
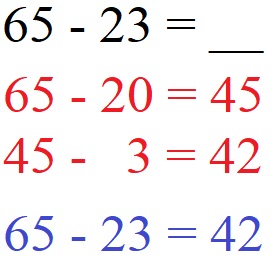
Beispiel 4: Halbschriftliche Subtraktion
Die halbschriftliche Subtraktion funktioniert auch wenn die Zahlen dreistellig sind. Im Beispiel soll 423 - 214 berechnet werden. Die 214 wird zerlegt in 200, 10 und 4. Danach wird einzeln subtrahiert (minus gerechnet).
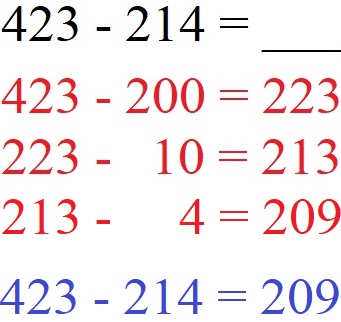
Die halbschriftliche Subtraktion wird meistens im Zahlenraum bis 1000 verwendet. Werden die Zahlen noch größer wird die schriftliche Subtraktion eingesetzt.
Halbschriftliche Multiplikation
Eine weitere Grundrechenart ist die Multiplikation. Für diese gibt es ebenfalls eine halbschriftliche Rechnung. Die halbschriftliche Multiplikation wird oft ab der 3. Klasse der Grundschule behandelt.
Beispiel 5: Halbschriftliche Multiplikation
In diesem Beispiel soll 8 · 23 berechnet werden. Wir zerlegen die zweistellige Zahl in 20 und 3. Danach rechnen wir 8 · 20 = 160 und 8 · 3 = 24. Die addieren wir im Anschluss und bekommen 160 + 24 = 184.
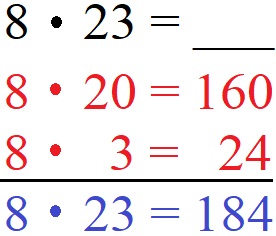
Beispiel 6: Halbschriftliche Multiplikation
Die halbschriftliche Multiplikation funktioniert auch wenn eine Zahl dreistellig ist. In diesem Fall soll 5 · 123 ausgerechnet werden. Die 123 zerlegen wir in Hunderter (100), in Zehner (20) und Einer (3) und multiplizieren mit der 5. Die Ergebnisse addieren wir: 500 + 100 + 15 = 615.
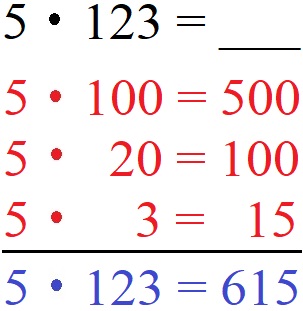
Halbschriftliche Division
Als letzte Grundrechenart bleibt noch die Division oder für hier das halbschriftliche Dividieren. Wir starten mit einer Einführung in das halbschriftliche Dividieren und sehen uns dabei die Grundlagen an. Die halbschriftliche Division wird in der 3. Klasse und 4. Klasse der Grundschule in Mathematik behandelt.
Beispiel 7: Halbschriftliche Division
Berechnet werden soll 384 : 6. Wir zerlegen die erste Zahl, also die 384 in drei Zahlen, die wir einfach durch 6 teilen können. Es gibt mehrere Möglichkeiten dies zu tun. Für dieses Beispiel wurde die 384 zerlegt in 300, in 60 und in 24. Diese drei Zahlen teilen wir jeweils durch 6. Die Quotienten werden addiert: 50 + 10 + 4 = 64.

Beispiel 8: Halbschriftliche Division
Die dreistellige Zahl 896 soll durch 8 geteilt werden. Dabei zerlegen wir die erste Zahl (Dividend) in 800, 80 und 16. Diese drei Zahlen lassen sich einfach durch 8 (Divisor) teilen. Die Ergebnisse addieren wir: 100 + 10 + 2 = 112.

Aufgaben (Übungen) halbschriftliches Rechnen
136 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: