Kreiskegel ( gerader, schiefer )

Mit dem Kreiskegel befassen wir uns in diesem Artikel. Dabei zeigen wir euch Formeln zur Berechnung von Volumen, Oberfläche etc. eines Kreiskegels inklusive Beispiele. Dieser Artikel gehört zu unserem Bereich Mathematik.

Stellt sich zunächst einmal die Frage, was ein Kreiskegel überhaupt ist? Nun, ein gerader Kreiskegel hat den Radius r als Grundfläche, die Spitze liegt in der Höhe h senkrecht über dem Mittelpunkt des Kreises. Die folgende Grafik zeigt euch, wie so ein gerader Kreiskegel aussieht und führt auch schon die entsprechenden Variablen für die Formeln ein.

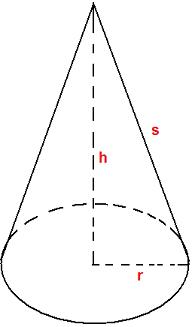
Kreiskegel Formeln: Volumen, Oberfläche, Mantelfläche etc.

In diesem Abschnitt befassen wir uns mit den Formeln zum Kreiskegel.  Gerade und schiefe Kreiskegel haben genau dann das gleiche Volumen, wenn sie die gleiche Grundfläche und die gleiche Höhe haben. Zu den Formeln für den geraden Kreiskegel:

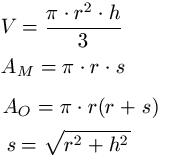
Dabei ist:

• "V" das Volumen des Kreiskegels
• "π" die Kreiszahl, etwa 3,14159
• "r" der Radius der Grundfläche
• "h" die Höhe des Kreiskegels
• "A_M" die Mantelfläche
• "A_O" die Oberfläche
• "s" ist die Länge der Seite

Kreiskegel Berechnung Beispiele

In diesem Abschnitt befassen wir uns noch mit einigen Beispielen zum Kreisegel, welche die Berechnung wichtiger Größen zeigt.

Beispiel 1:

Ein Kreiskegel hat einen Radius von 80cm und eine Höhe von 4m. Berechne sein Volumen. Lösung: Wir wandeln zunächst die cm-Angaben in Meter-Angaben um, damit wir die Angaben in gleichen Einheiten in die Formel einsetzen können. Und damit berechnen wir dann das Volumen.

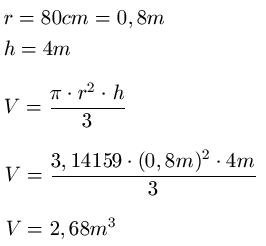
Beispiel 2:

Ein Kreiskegel hat einen Radius von 40cm und eine Höhe von 60cm. Berechne die Mantelfläche und die Oberfläche. Lösung: Wir berechnen zunächst die Länge der Seite "s", da wir diese Angaben für die weitere Berechnung benötigen. Danach müssen wir nur noch in die anderen Formeln die Werte einsetzen und alles ausrechnen.

Links:

• Zur Mathematik-Übersicht