Lineare Funktion durch 2 Punkte

In diesem Artikel geht es darum mit zwei Punkte eine lineare Funktion / Gerade zu bestimmen. Dies wird durch einige Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Manchmal sucht man im Mathematik-Unterricht eine Funktion. Dann sind verschiedene Punkte gegeben und damit soll eine Funktion bestimmt werden, die genau durch diese Punkte verläuft. Um die nächsten Abschnitte zu verstehen solltet ihr wissen was eine lineare Funktion ist und wie man ein lineares Gleichungssystem löst.

• Lineare Funktion
• Lineares Gleichungssystem lösen

Gerade / Lineare Funktion durch 2 Punkte

Eine Gerade oder auch eine lineare Funktion beschreibt man mit f(x) = y = mx + b. Die Variablen m und b sind unbekannt. Um diese zu bestimmen benötigen wir zwei Punkte. Damit stellen wir zwei Gleichungen auf und lösen das lineare Gleichungssystem um m und b zu bestimmen. Dies soll nun durch Beispiele gezeigt werden.

Beispiel 1:

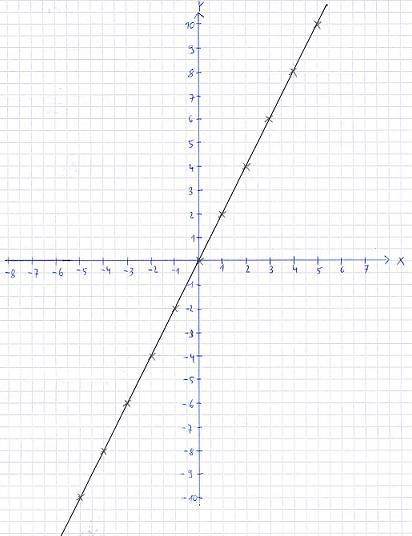
Auf der folgenden Grafik seht ihr eine lineare Funktion. Gesucht ist eine mathematische Beschreibung dieses Verlaufs. Dazu lesen wir zunächst zwei Punkte auf der Grafik ab. Dies wären zum Beispiel P₁ ( 0 | 0 ) und P₂ ( 1 | 2 ). Wir haben also zwei Punkte mit jeweils einem X-Wert und einem Y-Wert. Wir setzen beide Punkte in y = mx + b ein. Wir erhalten damit zwei Gleichungen:

• P₁: 0 = m · 0 + b
• P₂: 2 = m · 1 + b

Durch die erste Gleichung sehen wir, dass b = 0 ist. Setzen wir dies in die zweite Gleichung ein, erhalten wir noch m = 2. Damit erhalten wir nach Einsetzen in y = mx + b:

• y = 2x + 0

Beispiel 2:

Gegeben sind zwei Punkte mit P₁ ( 2 | 3 ) und P₂ ( 5 | 6 ). Wie lautet die zugehörige lineare Funktion?

Lösung: Wir setzen beide Punkte in y = mx + b ein und lösen das lineare Gleichungssystem im Anschluss.

• P₁: 3 = m · 2 + b
• P₂: 6 = m · 5 + b

• 3 = 2m + b
• 6 = 5m + b

Wir stellen die erste Gleichung nach b um:

• 3 = 2m + b
• 3 - 2m = b

Und setzen dies in die zweite Gleichung ein:

• 6 = 5m + b
• 6 = 5m + 3 - 2m
• 3 = 3m
• m = 1

Mit m = 1 gehen wir in die erste Gleichung:

• 3 = 2m + b
• 3 = 2 · 1 + b
• 3 = 2 + b
• b = 1

Mit b = 1 und m = 1 erhalten wir:

• y = mx + b
• y = x + 1

Links:

• Zur Mathematik-Übersicht