y = mx + b oder y = mx + n

Was will der Mathematik-Lehrer eigentlich mit seinem y = mx + b oder y = mx + n? Genau dies erklären wir in den folgenden Zeilen und stellen auch Beispiele vor. Dieser Artikel gehört zu unserem Bereich Mathematik.

Um die folgenden Inhalte gut verstehen zu können, sind ein paar Vorkenntnisse sinnvoll. Wer die folgenden Themen noch nicht kennt, möge diese bitte erst einmal nachlesen:

• Lineare Gleichungen
• Variablen und Formeln
• Lineares Gleichungssystem

Was ist y = mx + b?

Eine Gerade bzw. auch eine lineare Funktion beschreibt man mit f(x) = y = mx + b. Dabei sind m und b Unbekannte, sprich Variablen. Manchmal steht anstelle von b auch n oder irgend ein anderer Buchstabe (Variable). Das spielt aber keine Rolle. Wichtig ist zu wissen, dass man damit eine lineare Funktion beschreibt. Um dieses y = mx + b bestimmen zu können, benötigen wir zwei Punkte. Diese setzen wir ein, erhalten ein Gleichungssystem und lösen dieses im Anschluss. Klingt kompliziert, ist eigentlich aber gar nicht so schwer. Die folgenden Aufgaben zeigen, wie es geht.

Beispiel 1:

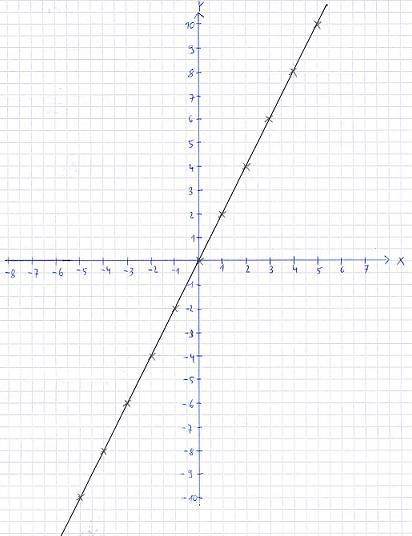
Die folgende Grafik zeigt eine Gerade. Gesucht ist eine mathematische Beschreibung dieses Verlaufs. Dazu lesen wir zunächst zwei Punkte ab. Dies wären zum Beispiel P₁ (0|0) und P₂ (1|2). Wir haben also zwei Punkte mit jeweils einem x-Wert und einem y-Wert. Dies setzen wir in in y = mx + b ein. Wir erhalten damit zwei Gleichungen:

• P₁: 0 = m · 0 + b
• P₂: 2 = m · 1 + b

Bei der ersten Gleichung sehen wir sofort, dass b = 0 sein muss. Setzen wir dies in die zweite Gleichung ein, erhalten wir noch m = 2. Damit erhalten wir nach Einsetzen in y = mx + b:

• y = 2x + 0

Beispiel 2:

Nehmen wir zwei andere Punkte, zum Beispiel P₁ (2|3) und P₂ (5|6). Wie lautet die zugehörige lineare Funktion?

Lösung: Wir setzen erneut in y = mx + b ein und lösen das Gleichungssystem, um m und b zu bekommen.

• P₁: 3 = m · 2 + b
• P₂: 6 = m · 5 + b

• 3 = 2m + b
• 6 = 5m + b

Wir stellen die erste Gleichung nach b um:

• 3 = 2m + b
• 3 - 2m = b

Und setzen dies in die zweite Gleichung ein:

• 6 = 5m + b
• 6 = 5m + 3 - 2m
• 3 = 3m
• m = 1

Und mit m = 1 gehen wir in die erste Gleichung:

• 3 = 2m + b
• 3 = 2 · 1 + b
• 3 = 2 + b
• b = 1

Mit b = 1 und m = 1 erhalten wir:

• y = mx + b
• y = x + 1

Wie man sehen kann, beschreibt man eine lineare Gleichung mit y = mx + b oder y = mx + n. Durch Einsatz entsprechender Punkte kann man m und b bzw. n bestimmen.

Links:

• Zur Mathematik-Übersicht