Logarithmieren

Mit dem Logarithmieren befassen wir uns in diesem Artikel. Dabei erklären wir euch, was man unter dem logarithmieren versteht und wie es funktioniert. Außerdem erhaltet ihr einige passende Beispiele und Rechengesetze.

Die meisten von euch mussten sicher schon Gleichungen oder sogar ganze Gleichungssysteme lösen. Dabei hatte man z.B. eine Gleichung der Form 2 + 5x = 0 nach x aufzulösen. Dies wurde durch Addition, Subtraktion, Multiplikation und Division gelöst. Aber angenommen, ihr sollt  y = 2^x nach x auflösen. Was dann? Die Antwortet lautet: Logarithmus anwenden. Genau darum kümmern wir uns in diesem Abschnitt. Doch zuvor solltet Ihr sicherstellen, dass Ihr die folgenden Themen kennt. Wer mit diesen noch Probleme hat, folgt den Links. Alle anderen können gleich mit dem Logarithmus loslegen.

• Potenzen
• Gleichungen lösen
• Exponentialfunktionen

Logarithmieren: Der Zweierlogarithmus

Schauen wir uns noch einmal das Beispiel von eben an: y = 2^x. Diese Gleichung soll nun nach x aufgelöst werden. Wir logarithmieren aus diesem Grund die Gleichung wie folgt:

Tabelle nach rechts scrollbar

Wie bei jeder Gleichung gilt: Was man links macht, muss man auch rechts machen. Somit wird der Logarithmus auf beiden Seiten angewendet.  log₂y = x bedeutet: Der Logarithmus von y zu Basis 2 ist gleich x. Ihr müsst euch also folgendes überlegen: Welche Hochzahl x benötige ich, mit der die Zahl 2 potenziert werden muss, damit man y erhält. Das Beispiel von eben hat den Zweierlogarithmus gezeigt, denn die Basis war eine 2. Es folgt die allgemeine Gleichung, dann schauen wir uns ein paar Beispiele zum besseren Verständnis an.

Allgemein gilt:

y = log_ax <=> x = a^y

Beispiele:

• log₂16 = 4, denn 2⁴ = 16
• log₂1024 = 10, denn 2¹⁰ = 1024

Logarithmieren: Natürlicher und dekadischer Logarithmus

Bevor wir mit dem natürlichen Logarithmus loslegen, erst noch eine kleine Erinnerung: Eine E-Funktion hat die Form e^ax, also zum Beispiel e^2x oder e^5x. Das e ist die sogenannte eulersche Zahl, welche in vielen Naturwissenschaftlich-Technischen Funktionen auftritt. In der Gleichung gilt e = 2,718. Wir setzen also nun die 2,718 für das e in die Gleichung ein.

Wir haben weiter oben im Artikel bereits das Rechnen mit der Basis 2 sowie in den Formeln auch mit allgemeiner Basis gearbeitet ( Siehe dazu die Rechenregeln und Beispiele in der Tabelle ). In der Mathematik wurden für die Basis 10 und die Basis e ( eulersche Zahl noch zwei verschiedene Namen vergeben.

Logarithmieren: Natürlicher Logarithmus

Hat man die Basis e, so führt dies zum natürlichen logarithmus. Die Form: log_ex. Dafür existiert auch eine abgekürzte Schreibweise: Diese lautet lnx. Welche Schreibweise ihr bevorzugt, ist euch überlassen ( oder wird vom Mathematik-Lehrer vorgegeben ).

Merke: log_ex = lnx

Dekadischer Logarithmus

Hat man hingegen die Basis 10, führt dies zum dekadischen Logarithmus oder auch Zehnerlogarithmus genannt. Die Form log₁₀r. Auch hier existiert eine Abkürzung: lg r.

Merke: log₁₀r = lgr

Die Logarithmus Regeln

Im nun folgenden findet ihr die Regeln des Logarithmus für Produkte, Brüche, Potenzen, Wurzeln sowie die Umrechnung zwischen Logarithmensystemen.

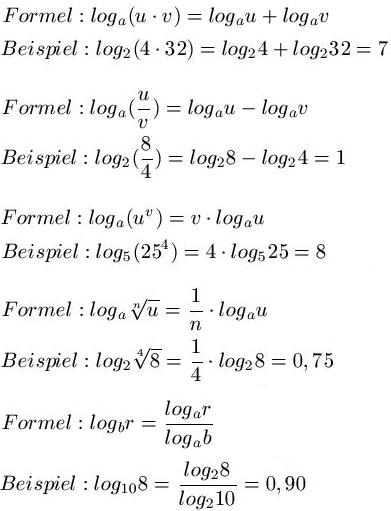
Links:

• Übungen: Logarithmus
• Zurück zur Mathematik-Übersicht