Matrix und Matrizen Grundlagen

Dieser Artikel beschäftigt sich mit dem Begriff der Matrix  bzw. mit dem Einsatz von Matrizen. Dabei sollen hier zunächst einmal die absoluten Grundlagen zu diesem Bereich der Mathematik gelegt werden.

Viele erinnern sich hoffentlich noch an Aufgaben zu linearen Gleichungssystemen. Wem dies nichts mehr sagt, der klickt sich noch einmal kurz in unseren Artikel Lineare Gleichungssysteme. War das Gleichungssystem sehr groß, wurde die Schreibarbeit zur Berechnung der Unbekannten sehr aufwändig und fehleranfällig. Eine Matrix hilft derartige Aufgaben schneller zu lösen. Zu dem wird das Wissen über Matrizen auch noch in der Vektorrechnung benötigt.  Dieser Artikel soll jedoch erst einmal den Aufbau einer Matrix und einige Eigenheiten erläutern.

Die folgende Grafik zeigt euch die allgemeine Schreibweise einer Matrix. Dies mag auf den ersten Blick abschreckend wirken, ist aber eigentlich ganz einfach. Seht sie euch erst einmal an:

Einige Erklärungen zu dieser Matrix-Schreibweise:

• Eine Matrix hat m-Zeilen. Dabei steht "m" für die Anzahl der Zahlenwerte, die untereinander stehen. Die Zeilen einer Matrix werden oft auch als Zeilenvektoren bezeichnet.
• Eine Matrix hat n-Spalten. Dabei steht "n" für die Anzahl der Zahlenwerte, die nebeneinander stehen. Die Spalten einer Matrix werden oft auch als Spaltenvektoren bezeichnet.
• Folglich hat eine Matrix m · n Zahlen.
• Besitzt eine Matrix nur eine Spalte, wird sie als Spaltenmatrix bezeichnet.
• Besitzt eine Matrix nur eine Zeile, wird sie als Zeilenmatrix bezeichnet.
• a_ik wird als Matrixelement bezeichnet

Matrix Beispiele:

Die folgenden Beispiele werden euch hoffentlich helfen, den Aufbau und das Verständnis zu einer Matrix zu verbessern. Seht euch dazu das Beispiel gründlich an und lest die Erklärungen dazu aufmerksam durch.

Beispiel 1:

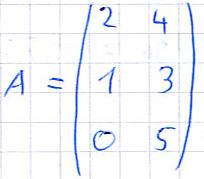
Diese Matrix besitzt 3 Zeilen und 2 Spalten. Ihre Elemente lauten wie folgt: a₁₁ = 2 , a₁₂ = 4, a₂₁ = 1, a₂₂ = 3, a₃₁ = 0 und a₃₂ = 5.

Beispiel 2:

Diese Matrix besitzt 3 Zeilen und 4 Spalten. Ihre Elemente lauten wie folgt: a₁₁ = 3, a₁₂ = 1, a₁₃ = 2, a₁₄ = 4, a₂₁ = 2, a₂₂ = 0, a₂₃ = 5, a₂₄ = 1, a₃₁ = 8, a₃₂ = 2, a₃₃ = 1 und a₃₄ = 2.

Links:

• Zur Mathematik Übersicht