Normalenvektor ( Gerade / Ebene )

Mit dem Normalenvektor einer Gerade bzw. dem Normalenvektor einer Ebene befassen wir uns in diesem Artikel. Dabei erklären wir euch, was ein Normalenvektor überhaupt ist und wie man diesen bildet. Dieser Artikel gehört zum Bereich Mathematik.

Zunächst eine kurze Definition: In der Geometrie ist ein Normalenvektor ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene oder (gekrümmten) Fläche steht. Die Gerade, die diesen Vektor als Richtungsvektor besitzt, heißt Normale. Im nun Folgenden zeigen wir euch dies anhand einer Gerade und einer Ebene.

Normalenvektor einer Geraden

In der folgenden Grafik seht ihr eine allgemeine, parameterfreie Gleichung einer Geraden g in der Ebene. Aus dieser wird der Normalenvektor "n" abgelesen.

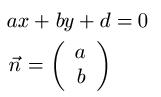
Beispiel:

Gegeben sei die Gleichung einer Geraden mit  2x - 3y -5 = 0. Wie lautet der Normalenvektor?

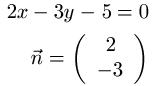
Normalenvektor einer Ebene

In der folgenden Grafik seht ihr eine allgemeine, parameterfreie Gleichung einer Ebene. Aus dieser wird der Normalenvektor "n" abgelesen.

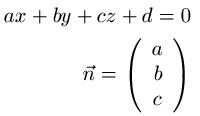
Beispiel 1:

Gegeben sei eine Ebene mit der Gleichung 2x + 3y -5z + 2 = 0. Wie lautet der Normalenvektor?

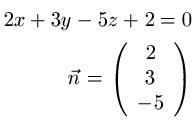
Beispiel 2:

Gegeben sei die Gleichung einer Ebene in Parameterfom. Ein Normalenvektor dieser Ebene soll bestimmt werden.

Lösung: Wir wandeln die Gleichung der Ebene zunächst in Koordinatenform um. Zum besseren Verständnis wird diese Lösung komplett hergeleitet. Wem dies nicht genügend, der sieht bitte in unseren Artikel Parametergleichung in Koordinatengleichung wandeln. Aus der Koordinatenform lesen wir im Anschluss den Normalenvektor ab.

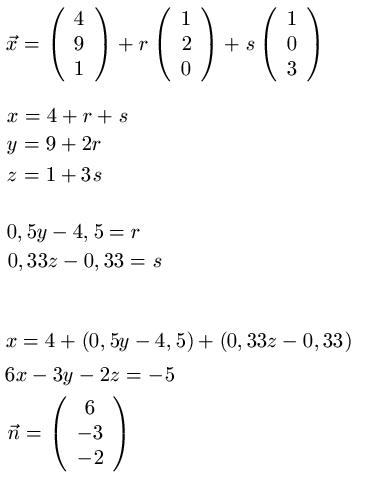
Links:

• Zur Mathematik-Übersicht