Das Parallelogramm der Mathematik lernst du hier erkennst. Du bekommst zunächst eine schnelle Übersicht über das Parallelogramm. Im Anschluss sehen wir uns Beispiele und Formeln zu Umfang, Flächeninhalt, Höhe und Winkel des Parallelogramms an. Wie ein Parallelogramm gezeichnet wird und den Unterschied zu Trapez, Rechteck und Quadrat bekommst du ebenfalls.
Ein Parallelogramm ist ein Viereck bei dem gegenüberliegenden Seiten parallel und gleich lang sind. Parallelogramme sind damit spezielle Trapeze. Ein anderes Wort für Parallelogramm ist Rhomboid.
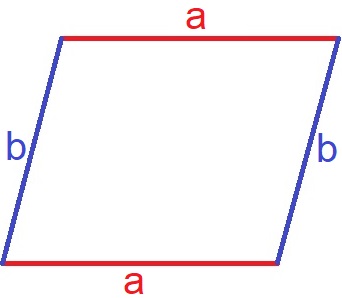
Im nächsten Abschnitt sehen wir uns Eigenschaften bzw. Merkmale vom Parallelogramm an. Danach geht es an Erklärungen und Beispiele zu Umfang, Flächeninhalt, Winkeln und Höhe vom Parallelogramm. Du erfährst auch wie ein Parallelogramm gezeichnet wird und den Unterschied zu anderen Vierecken.
Parallelogramm Eigenschaften und Merkmale
Ein Parallelogramm hat folgenden Eigenschaften bzw. Merkmale:
- Es ist ein Viereck, hat demnach vier Ecken.
- Es hat vier Winkel (Alpha, Beta, Gamma und Delta).
- Gegenüberliegende Seiten sind parallel.
- Gegenüberliegende Seiten sind gleich lang.
- Zwei benachbarte Winkel ergeben in Summe 180 Grad.
- Gegenüberliegende Winkel sind gleich groß.
- Die Summe der 4 Innenwinkel beträgt 360 Grad.
Die Eckpunkte von einem Quadrat werden mit A, B, C und D bezeichnet. Die Seiten werden mit a und b angegeben.
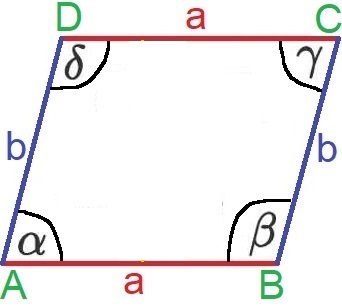
Das Parallelogramm hat eine Höhe h, welche den Abstand der beiden Seiten a angibt. In manchen Darstellungen wird diese Höhe auch ha genannt.
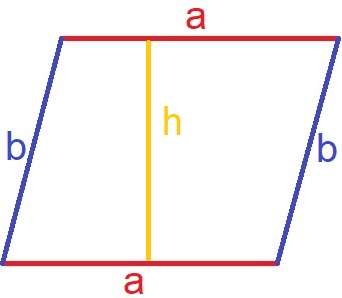
Die gegenüberliegenden Ecken können verbunden werden. Es entstehen dadurch zwei Diagonale mit einem Schnittpunkt. Diese Diagonalen werden oft mit e und f bezeichnet.
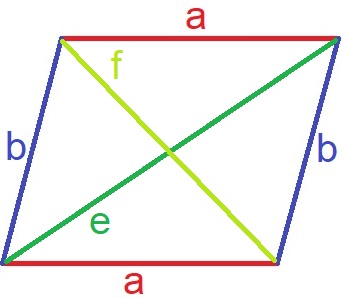
Mit diesem Grundwissen sehen wir uns im nächsten Abschnitt den Umfang an.
Umfang Parallelogramm: Formel mit Beispiel
Der Umfang des Parallelogramms ist die Summe der vier Seiten, welche dieses Viereck begrenzen. Die gegenüberliegenden Seiten sind dabei gleich lang, daher kommt die Strecke "a" zwei Mal vor, ebenso die Strecke "b".
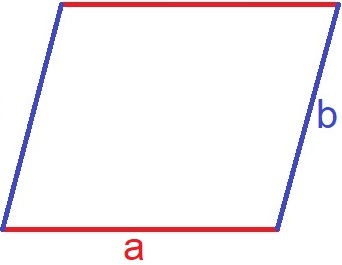
Die Formel zum Umfang lautet:
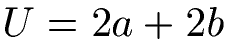
Die Formel entspricht damit der Formel wie sie auch für den Umfang von einem Rechteck verwendet wird.
Parallelogramm Umfang Beispiel:
Die Seite "a" sei 4 Meter lang, die Seite "b" sei 3 Meter lang. Wie groß ist der Umfang des Parallelogramms? Zur Lösung setzen wir die Angaben in die Formel für den Umfang ein.
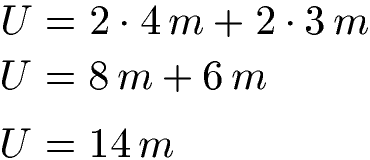
Ein Parallelogramm mit den Seitenlängen 4 Meter und 3 Meter hat einen Umfang von 14 Metern.
Flächeninhalt Parallelogramm: Formel mit Beispiel
Der Flächeninhalt eines Parallelogramms kann auf verschiedenen Wegen berechnet werden. Im einfachsten Fall ist die Seitenlänge "a" und die Höhe "h" bekannt.
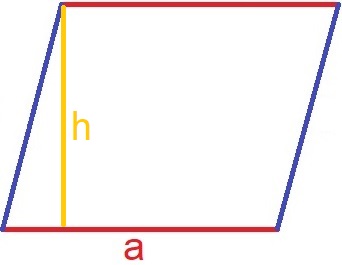
Der Flächeninhalt berechnet sich aus Seitenlänge "a" multipliziert mit der Höhe "h":
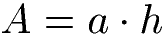
Parallelogramm Flächeninhalt Beispiel:
Die Seite "a" sei 5 Meter lang und die Höhe "h" sei 3 Meter. Wie groß ist die Fläche? Zur Lösung setzen wir beide Angaben in die Formel ein. Beachtet das Meter (m) mal Meter (m) zu Quadratmeter (m2) werden.
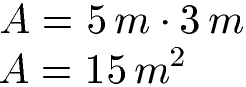
Sollte dir die Höhe fehlen, lernst du im nächsten Abschnitt diese zu berechnen.
Der Flächeninhalt lässt sich auch aus der Länge der Seiten "a" und "b" und dem Winkel Alpha berechnen.
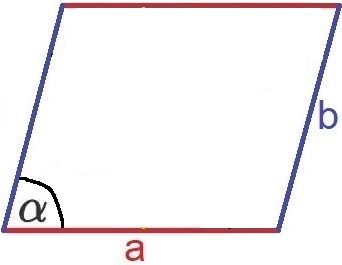
Die Formel zur Berechnung der Fläche mit Winkel lautet:
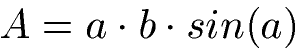
Flächeninhalt Parallelogramm mit Winkel:
Die Seitenlängen eines Parallelogramms seien 4 Meter und 5 Meter, der Winkel Alpha ist 75 Grad groß. Wie groß ist der Flächeninhalt? Zur Lösung setzen wir die drei Angaben in die Formel ein. Stelle bei der Berechnung von sin(75) im Taschenrechner diesen auf DEG (um kein falsches Ergebnis zu erhalten).
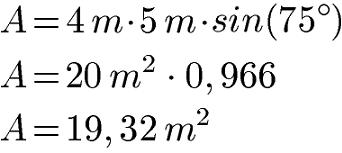
Im nächsten Abschnitt sehen wir uns mehr zum Berechnen von Höhe und Winkel im Parallelogramm an.
Winkel und Höhe im Parallelogramm
Die Höhe "h" in einem Parallelogramm lässt sich mich mit der Länge der Seite b und dem Winkel Alpha berechnen. Die Bezeichnungen beziehen sich auf diese Grafik:
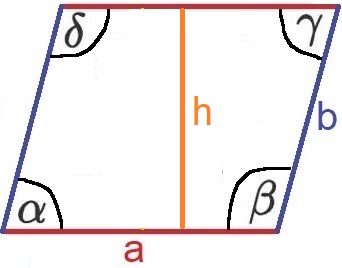
Die Formel um die Höhe "h" zu berechnen lautet:
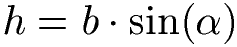
Parallelogramm Höhe berechnen Beispiel:
Die Länge "b" sei 4 Meter lang und der Winkel Alpha sei 70 Grad groß. Wie groß ist die Höhe des Parallelogramms? Zur Lösung setzen wir beide Angaben in die Formel ein. Für die Berechnung muss der Taschenrechner auf DEG gestellt werden.
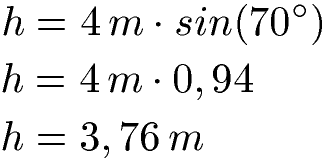
Winkel berechnen:
Um Winkel im Parallelogramm zu berechnen, findest du hier eine Reihe an Formeln und Zusammenhänge im Parallelogramm.
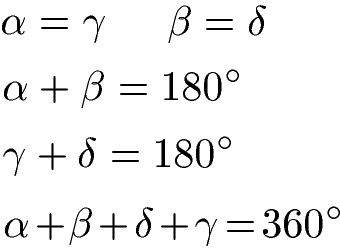
Winkel berechnen Beispiel:
Um die Höhe im Parallelogramm zu berechnen, fehlt der Winkel Alpha. Jedoch ist Beta mit 110 Grad bekannt. Da sich die beiden Winkel zu 180 Grad ergänzen, lässt sich Alpha mit 70 Grad berechnen.
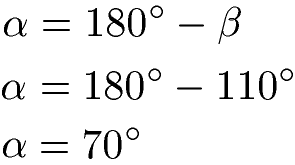
Diagonale im Parallelogramm
Die gegenüberliegenden Seiten im Parallelogramm lassen sich verbinden. Diese Verbindungen werden Diagonale genannt und Schneiden sich innerhalb des Parallelogramms. Die Diagonalen werden in Zeichnungen und Formeln oft mit "e" und "f" bezeichnet.
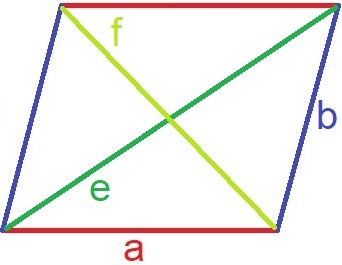
Die Längen der Diagonalen lassen sich über die folgenden Formeln berechnen.
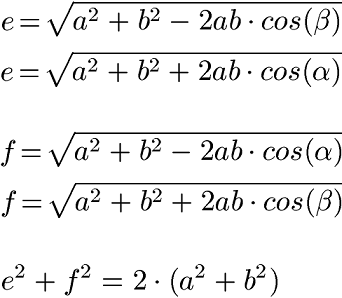
Parallelogramm zeichnen
Es gibt verschiedene Möglichkeiten ein Parallelogramm zu zeichnen. Welches Vorgehen verwendet wird hängt stark davon ab, welche Informationen gegeben sind. Angenommen die Längen a und b sowie der Winkel Alpha sind gegeben. In diesem Fall lässt sich das Parallelogramm wie folgt zeichnen.
Zeichne zunächst die Länge "a".
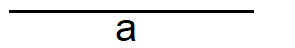
Lege das Geodreieck links an "a".
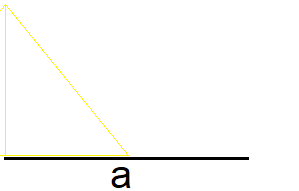
Soll der Winkel beispielsweise 80 Grad groß sein, markiere dir diesen Punkt auf dem dem Papier.
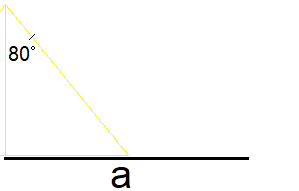
Zeichne vom Anfang von "a" aus in Richtung der Markierung für die Länge die für "b" vorgegeben ist.
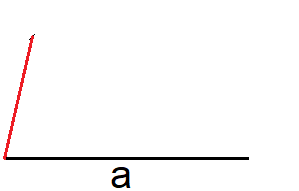
Zeichne die Länge "a" an die Länge "b" an, parallel zur ersten Strecke.
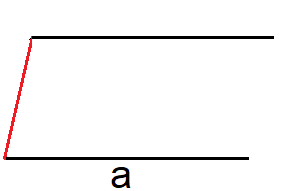
Vervollständige das Parallelogramm.
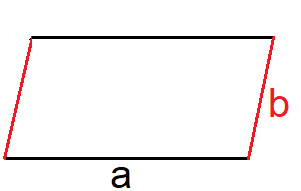
Parallelogramm zu Trapez, Rechteck oder Quadrat
Quadrat, Rechteck und Trapez sind spezielle Parallelogramme. In diesem Abschnitt sehen wir uns die Unterschiede und Gemeinsamkeiten an.
Ein Quadrat ist ein spezielles Parallelogramm. Beides sind Vierecke, jedoch sind beim Quadrat alle Winkel 90 Grad groß und alle Seiten sind gleich lang.
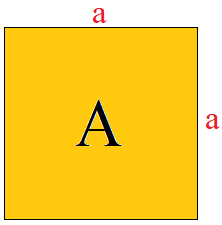
Ein Rechteck ist ein spezielles Parallelogramm. Beides sind Vierecke, jedoch sind beim Rechteck alle Winkel 90 Grad groß.

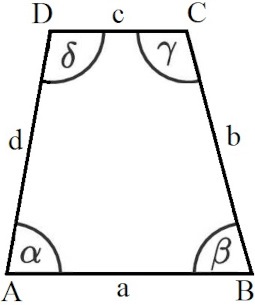
Ein Trapez und ein Parallelogramm haben ebenfalls viel gemeinsam. Beides sind Vierecke mit vier Winkeln. Jedoch reichen beim Trapez ein Paar paralleler Seiten aus, beim Parallelogramm sind hingegen zwei Paare paralleler Seiten nötig.
Weitere Links:
288 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: