Prisma: Formeln, Volumen etc.

Mit dem Prisma befassen wir uns in diesem Artikel. Dabei zeigen wir euch Formeln zur Berechnung von Volumen, Oberfläche etc. eines Prisma inklusive Beispiele. Dieser Artikel gehört zu unserem Bereich Mathematik.

Stellt sich zunächst einmal die Frage, was ein Prisma überhaupt ist? Ein Prisma ist ein geometrischer Körper, der ein Vieleck als Grundfläche hat und dessen Seitenkanten parallel und gleich lang sind. Ein Prisma entsteht durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum und ist daher ein spezielles Polyeder. Man unterscheidet oftmals zwischen geradem und schiefem Prisma, wobei die folgende Grafik ein gerades Prisma zeigt.

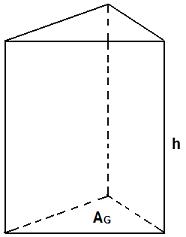
Prisma Formeln: Volumen, Oberfläche, Mantelfläche

In diesem Abschnitt befassen wir uns mit den Formeln zur Berechnung eines Prisma. Dazu liefern wir euch zunächst die Formeln inklusive der Beschreibung der Variablen sowie Beispiele zum besseren Verständnis. Beginnen wir mit den Formeln:

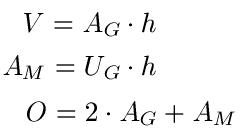
Dabei ist:

• "V" das Volumen des Prisma
• "A_G" die Grundfläche des Prisma
• "h" die Höhe des Prisma
• "A_M" ist die Mantelfläche
• "U_G" ist der Umfang der Grundfläche
• "O" ist die Oberfläche des Prisma

Beispiel 1:

Die Grundfläche des Prisma besteht aus einem rechtwinkligen Dreieck. Die Katheten sind 9cm und 12cm lang und die Höhe beträgt 20cm.  Das Volumen, die Mantelfläche und die Oberfläche sollen berechnet werden.

Lösung: Für die Berechnung des Volumens setzen wir natürlich die Formeln zur Volumenberechnung ein. Da es sich um ein rechtwinkliges Dreieck handelt, können wir hier mit der Formel für den Flächeninhalt eines Dreiecks arbeiten.

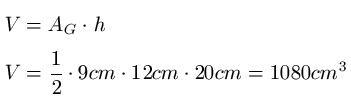
Als nächstes berechnen wir die Mantelfläche. Dazu benötigen wir den Umfang der Grundfläche. Die Längen der Katheten haben wir, fehlt also noch die Länge der Hypotenuse. Die Summe dieser drei Längen ist dann der Umfang der Grundfläche des Prisma. Diesen Wert multiplizieren wir mit der Höhe um A_M zu erhalten.

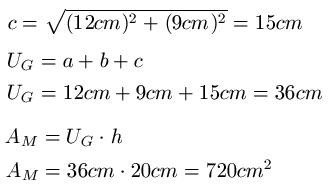
Als Letztes bestimmen wir die Oberfläche. Die Werte für A_G und A_M entnehmen wir vorigen Berechnungen um damit nun die Oberfläche zu bestimmen.

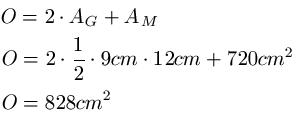
Links:

• Zur Mathematik-Übersicht