|
In diesem Abschnitt möchte ich Kurz und Knapp auf eine Sinus- und Kosinusschwingung eingehen. Wir kratzen dabei nur an der Oberfläche, um Schüler nicht gleich zu verschrecken. Neben Sinus und Kosinus geben wir hier zu dem noch einen Tangens-Funktionsgraphen an.
Wir haben uns im letzten Kapitel bereits mit den Winkelfunktionen Sinus, Kosinus und Tangens beschäftigt. In diesem Abschnitt geht es zwar immer noch um Sinus, Kosinus und Tangens. Jedoch kümmern wir uns hier um Schwingungen und Funktionsgraphen, welche diesen Namen tragen. Was es damit auf sich hat, erfahrt ihr im nun Folgenden:
Sinus - Funktion
Wir beginnen zunächst mit der Sinus-Funktion. Eine solche Funktion erhalten wir, wenn wir mit einem Messgerät an unsere Steckdose gehen und die Spannung aufzeichnen ( Details dazu in unserem Physik-Bereich ). Der nun folgende Graph zeigt einen Sinus-Verlauf der Funktion y = 1sin(x). Schaut euch die Grafik einmal an, Erklärungen finden sich darunter:
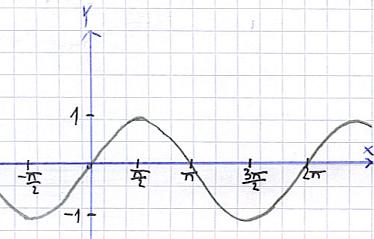
Erläuterungen: Wie auch bei normalen Gleichungen, kann man hier für das x verschiedene Werte einsetzen. In unserem Beispiel setzt man am Besten die Werte 0, π/2, π, 3π/2 und 2π in die Gleichung ein ( Taschenrechner auf RAD stellen ). Dadurch erhält man die oben gezeigte Funktion.
Anmerkung: Je nach Mathelehrer und Bundesland können noch Begriffe wie Amplitude, Schwingdauer, Frequenz und Phase im Unterricht auftauchen. Wer hier noch Informationen braucht, schaut in unseren Physik-Bereich.
Kosinus / Cosinus - Funktion
Schauen wir uns als nächstes die Kosinus / Cosinus-Funktion an. Die folgende Grafik zeigt den Verlauf für y = cos(x). Auch hier wurden wieder Werte eingesetzt, um die Funktion zu zeichnen. Der einzige Unterschied zur Sinus-Funktion ist, dass der Kosinus um π/2 verschoben wurde. Die sonstige "Gestalt" sieht gleich aus.
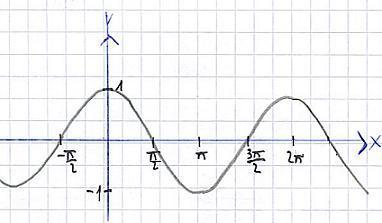
Auch hier wieder eine Anmerkung: Je nach Mathelehrer und Bundesland können noch Begriffe wie Amplitude, Schwingdauer, Frequenz und Phase im Unterricht auftauchen. Wer hier noch Informationen braucht, schaut in unseren Physik-Bereich.
Tangens-Funktion:
Zu guter Letzt noch der Verlauf des Tangens. Dabei handelt es sich nicht um eine Schwingung, sondern einfach um einen Funktionsgraphen. Zur Erinnerung: Der Tangens ergibt sich, in dem man sin(x) : cos(x) berechnet. Und genau dies wird bei einem solchen Verlauf gezeichnet und sieht wie folgt aus:
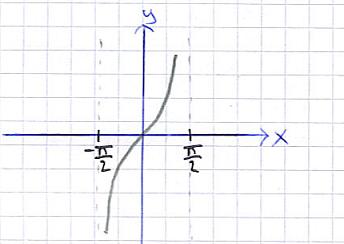
Links:
|
