Mit dem Sinussatz befassen wir uns in diesem Artikel. Dabei erklären wir euch, wozu man den Sinussatz benötigt und liefern euch passende Beispiele. Zu dem gehen wir auf die Herleitung / den Beweis des Sinussatzes ein. Dieser Artikel gehört zum Bereich Mathematik.

In der Trigonometrie stellt der Sinussatz eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten her. Die  Formeln zum Sinussatz beziehen sich auf die folgende Grafik:

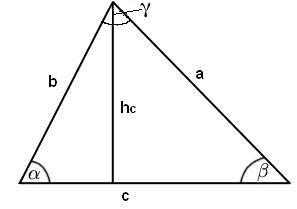
Sinussatz Formeln:

In jedem Dreieck verhalten sich die Längen zweier Seiten wie die Sinuswerte der gegenüberliegenden Winkel:

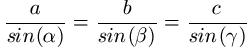
Häufig wird der Sinussatz auch als Verhältnisgleichung formuliert:

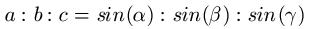
Beispiel:

Bekannt seien die Längen a = 5cm, b = 4cm und der Winkel α = 70 Grad. Der Winkel β soll berechnet werden.

Lösung: Wir entnehmen dem Text die Angaben und setzen diese in die Formel ein ( Erklärungen unterhalb ).

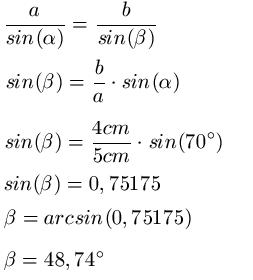
Wir stellen die Formel nach sin(β) um und setzen im Anschluss die Werte ein. Über den arcsin erhalten wie im Anschluss den Winkel.

Sinussatz Beweis / Herleitung

Zum Beweis des Sinussatzes benötigen wir Wissen aus dem Artikel Winkelfunktionen. Zurück zur Grafik: Die eingezeichnete Höhe h_c zerlegt das Dreieck in zwei rechtwinklige Teildreiecke. In diesen kann man die Sinuswerte von α und β jeweils als Quotient von Gegenkathete und Hypotenuse ausdrücken ( Erklärungen unterhalb ):

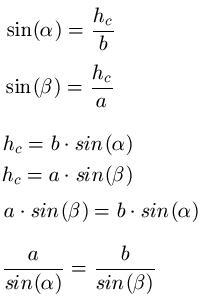
Zunächst werden die Sinuswerte als Quotient aus Gegenkathete und Hypotenuse ausgedrückt. Diese werden anschließend nach der Höhe umgestellt und gleichgesetzt. Durch Umformung erhalten wir die gewohnte Schreibweise.

Links:

• Zur Mathematik-Übersicht