Terme ▷ Mathematik

Was ein Term ist und was kein Term ist, lernst du in diesem Artikel mit Beispielen. Außerdem erfährst du welche Rechenregeln bei Termen verwendet werden und wie man Terme ohne Variablen und Terme mit Variablen berechnet. Die Inhalte liegen als Text und als Video vor.

Was versteht man unter einem Term? Starten wir dazu mit einer einfachen Definition zu einem Term:

Hinweis:
Ein Term ist eine sinnvolle mathematische Reihe aus Zeichen. Zeichen für gleich (=), kleiner (<) oder größer (>) dürfen nicht vorkommen!

Sehr einfache Beispiele für Terme sind einfache Rechenaufgaben. In diesen Aufgaben darf noch kein Istgleich (=) vorkommen. Erst beim Ausrechnen der Terme bzw. beim Vereinfachen der Terme kommt ein Istgleich vor.

Beispiele für Terme:

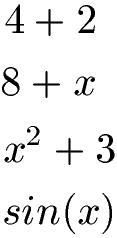
Keine Terme liegen vor wenn Relationszeichen vorhanden sind. Relationszeichen sind gleich (=), größer (>), kleiner (<) und ungleich (≠). Auch Aufgaben die "abgehackt" aussehen sind keine Terme. Fehlt zum Beispiel eine Zahl nach einem Additionszeichen oder eine Klammer liegt auch kein Term vor.

Keine Terme Beispiele:

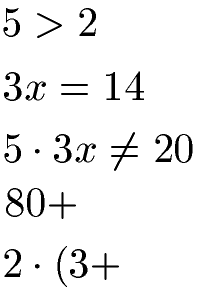
Es gibt Terme ohne Variablen und Terme mit Variablen. Beides sehen wir uns in den nächsten Abschnitten an.

Terme ohne Variablen: Rechenregeln

Unter einfachen Terme verstehen wir zunächst einmal Terme ohne Variablen. Für Terme mit Variablen und Terme ohne Variablen gelten die gleichen Rechenegeln. Daher macht es Sinn sich erst einmal die Rechenregeln ohne Variablen anzusehen.

Rechenregel: Von links nach rechts

Liegen nur Rechenzeichen mit gleicher Priorität vor wird einfach von links nach rechts gerechnet.

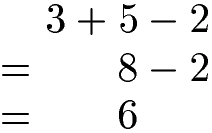
Rechenregel: Punkt vor Strich

Multiplikationen und Divisionen werden bei einer Aufgabe vor Additionen oder Subtraktionen berechnet. Die Regel wird Punkt vor Strich genannt. Im nächsten Beispiel wird daher erst multipliziert und danach addiert.

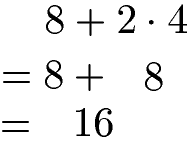
Rechenregel: Punkt vor Strich Beispiel 2

Eine Division wird ebenfalls vor einer Addition berechnet. Daher noch ein Beispiel mit einer Division innerhalb des Terms.

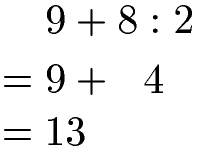
Rechenregeln für Terme mit Potenzen und Klammern

Insbesondere bei Potenzen und Klammern muss man bei der Reihenfolge der Berechnung sehr aufpassen. Sehen wir uns einige Beispiele an.

Regel: Klammer vor Punkt vor Strich

Eine wichtige Rechenregel bei Termen besteht darin, dass eine Klammer wird immer zuerst berechnet. Erst im Anschluss wird Punkt vor Strich eingesetzt. Daher immer erst der Inhalt in einer Klammer ausrechnen und diese im Anschluss auflösen. Im nächsten Beispiel wird daher erst die Addition in der Klammer berechnet und im Anschluss die Multiplikation.

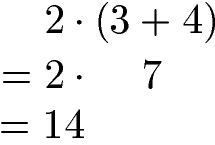
Rechenregel: Potenz vor Punkt vor Strich

Eine Klammer wird immer zuerst berechnet. Direkt nach der Klammer wird jedoch eine Potenz ausgerechnet. Daher erst die Potenz berechnen, in diesem Fall 2² = 2 · 2 = 4. Erst im Anschluss wird die Multiplikation durchgeführt.

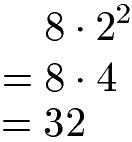
Regel: Potenzen vor Punkt vor Strich

Eine Potenz wird vor einer Addition berechnet. Im nächsten Beispiel wird daher erst 3² = 3 · 3 = 9 ausgerechnet und danach werden die Additionen von links nach rechts durchgeführt.

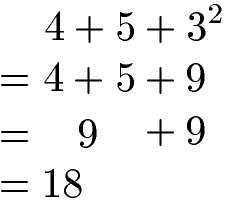
Im nächsten Abschnitt sehen wir uns die Rechenregeln für Terme mit Variablen an.

Terme zusammenfassen (mit Variablen)

Variablen (Buchstaben) sind Platzhalter. Für diese Platzhalter werden später einmal Zahlen eingesetzt. Gleiche Variable (= gleicher Buchstabe) bedeutet beim Einsetzen die gleiche Zahl einzusetzen.

Auch bei Termen können Variablen vorkommen. Diese können in vielen Fällen zusammengefasst werden. Die nächsten drei Beispiele zeigen wie man gleiche Variablen zusammenfassen kann.

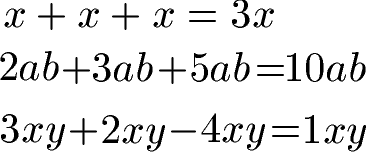
Terme mit verschiedenen Variablen:

Manchmal kommen in Termen unterschiedliche Variablen vor. In diesem Fall können die jeweils gleichen Variablen zusammengefasst werden. Im nächsten Beispiel wird nach den Variablen a und b unterschieden und jeweils zusammengefasst. Zum besseren Verständnis wurden diese farblich unterstrichen.

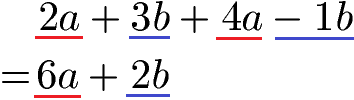
Es folgt noch ein Beispiel zu einem Term mit den Variablen x und y. Achtet bei der Berechnung sehr auf die Vorzeichen.

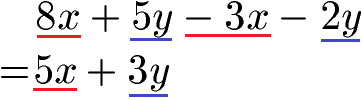
Im nächsten Abschnitt geht es noch um Terme mit Variablen bei denen auch Klammern vorkommen.

Terme vereinfachen (mit Variablen)

Welche Regeln gelten bei Termen mit Variablen und Klammern? Im Prinzip sind es genau die selben Regeln, welche auch bei Termen ohne Variablen eingesetzt werden müssen. Im nächsten Beispiel wird daher auch zuerst die Klammer berechnet und das Ergebnis mit 4a multipliziert.

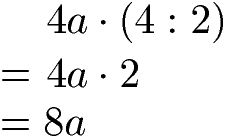
Kann eine Klammer nicht vereinfacht und damit aufgelöst werden, so versucht man diese auszumultiplizieren. Dazu wird die Zahl 3 vor der Klammer im nächsten Beispiel sowohl mit 2x als auch mit 4b multipliziert. Im letzten Schritt können noch gleiche Variablen zusammengefasst werden.

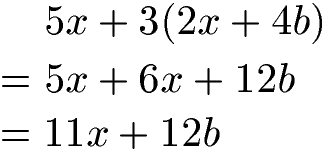
Fehlt noch ein Beispiel bei dem eine Potenz entsteht. Nach der Regel Punkt vor Strich wird zunächst 3x mit 4x multipliziert. Dabei entsteht 12x². Die Variablen x² und x sind verschieden und dürfen daher nicht zusammengefasst werden.

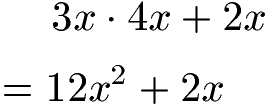
Links:

• Zur Mathematik-Übersicht