Tupel und Zählprinzip

Mit den Begriffen Tupel und Zählprinzip aus dem Bereich der Stochastik befassen wir uns in diesem Artikel. Dabei erklären wir euch, was man unter einem Tupel bzw. einem Zählprinzip für Mengen versteht und liefern euch passende Beispiele. Dieser Artikel gehört zum Bereich Mathematik.

Starten wir mit zwei Definitionen zu einem Tupel ( mathematisch + anschaulicher ):

1. Man definiert ein Tupel der Länge n als eine Aufzählung von n nicht notwendig von einander verschiedenen mathematischen Objekten in einer vorgegebenen, festen Reihenfolge.
2. Stellt man n Elemente einer Menge in einer bestimmten Reihenfolge zusammen und lässt man dabei auch Wiederholungen zu, so entsteht eine Folge der Länge k.

Beispiel:

Wir haben eine Folge von Buchstaben: ( a, c, c, n, x, y, y, z ) ist eine Folge der Länge 8 aus der Menge der Buchstaben unseres Alphabets.

Das Zählprinzip

Kommen wir nun zum Zählprinzip für Mengen. Dafür benötigt man den so genannten Binomialkoeffizient. Dieser gibt an, auf wie viele verschiedene Arten man k Objekte aus einer Menge von n verschiedenen Objekten auswählen kann. Der Versuch wird dabei ohne Zurücklegen und ohne Beachtung der Reihenfolge durchgeführt. Man könnte auch sagen: Die Anzahl der Möglichkeiten in einem n-Tupel genau k Plätze zu reservieren. Für das Zählprinzip bzw. die Berechnung des Binomialkoeffizienten gilt folgende Formel.

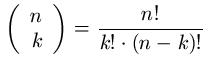
Beispiel:

In einer Urne befinden sich 30 Kugeln, die von 1 bis 30 durchnummiert sind. Aus der Urne sollen 6 Kugeln gezogen werden. Die gezogenen Kugeln werden nicht zurückgelegt und die Reihenfolge der Kugeln ist nicht von Interesse. Wie viele Möglichkeiten gibt es, diese Kugeln zu ziehen?

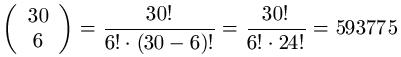
Links:

• Zur Stochastik-Übersicht
• Zurück zur Mathematik-Übersicht