Das Überschlagen bzw. die Überschlagsrechnung wird bereits ab der Grundschule im Mathematik-Unterricht behandelt. Es geht dabei sowohl um das Überschlagen mit den Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) als auch um das Überschlagen mit Dezimalzahlen (Kommazahlen) und Geld. Zum besseren Verständnis werden viele Beispiele vorgerechnet.
Starten wir mit einer Definition:
Hinweis:
Das Überschlagen dient dazu im Kopf eine grobe Vorstellung von der Lösung einer Mathematik-Aufgabe zu bekommen. Das Ergebnis der präzisen Rechnung muss daher in der Nähe des Überschlags liegen. Die Überschlagsrechnung dient auch dazu schwere Fehler bei der Berechnung mit dem Taschenrechner zu erkennen.
Die Überschlagsrechnung basiert auf dem Runden von Zahlen. Wer noch keine Ahnung hat wie man Zahlen auf Einer, Zehner oder Hunderter rundet, sollte erst einmal einen Blick auf das Thema Runden in der Mathematik werfen.
Überschlagsrechnung Addition
In der Klasse 3 und Klasse 4 der Grundschule geht es meistens mit dem Überschlagen von Zahlen los. Als Einführung dazu kann die Addition verwendet werden. Bei einfachen Beispielen werden zweistellige Zahlen gerundet und addiert.
Überschlag Beispiel 1 Addition:
Die zweistelligen Zahlen 58 und 33 sollen gerundet und addiert werden. In diesem Fall runden wir die Zahlen auf die Zehnerstelle. Um auf die Zehnerstelle zu runden sehen wir uns die Einerstelle an. Ist die Einerstelle 0, 1, 2, 3 oder 4 runden wir ab, ansonsten runden wir auf. Daher runden wir die 58 auf 60 auf und die 33 auf 30 ab. Danach addieren wir. Die Rechnung:
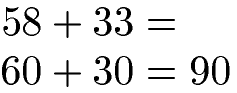
Überschlag Beispiel 2 Addition:
Dreistellige Zahlen können beispielsweise auf die Hunderterstelle gerundet werden. Dazu sehen wir uns die Zehnerstelle an: 0 bis 4 abrunden und 5 bis 9 aufrunden. Daher runden wir 112 auf 100 ab und 887 auf 900 auf. Die Summe daraus ist 1000.
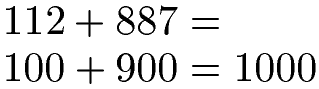
Überschlagen bei der Subtraktion
Bei Subtraktionsaufgaben (Minusaufgaben) kann ebenfalls mit einem Überschlag gearbeitet werden. Die Subtraktion beim Überschlagen wird oft in der 3. Klasse bzw. 4. Klasse der Grundschule behandelt.
Überschlag Beispiel 1 Subtraktion:
Überschlagen werden soll 48 - 23. Beim Runden auf die Zehnerstelle wird aus 48 eine 50, aus 23 wird 20. Die Überschlagsrechnung wird damit zu 50 - 20 = 30.
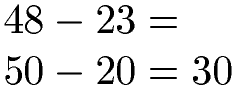
Überschlag Beispiel 2 Subtraktion:
Zwei dreistelligen Zahlen werden subtrahiert. In diesem Fall kann entweder auf die Zehnerstelle oder auf die Hunderterstelle gerundet werden. Hier nehmen wir einmal die Hunderterstelle. Daher achten wir auf die Zehnerstelle und runden bei 0 bis 4 ab und 5 bis 9 auf. Aus 505 wird 500 und aus 389 wird 400. Die Subtraktion ergibt 100.
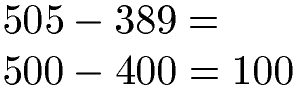
Multiplizieren mit Überschlagsrechnung
Gerade bei großen Multiplikationsaufgaben ist eine Überschlagsrechnung sehr sinnvoll. Gerade hier werden ganz schnell Rechenfehler gemacht und im Ergebnis fehlt eine 0 oder eine 0 ist zu viel.
Überschlag Beispiel 1 Multiplikation:
Die Zahlen 34 und 58 sollen gerundet und miteinander multipliziert werden. In diesem Fall runden wir die 34 auf 30 ab und die 58 auf 60 auf. Multiplizieren wir dies miteinander erhalten wir 3 · 6 = 18 und hängen zwei Nullen an.
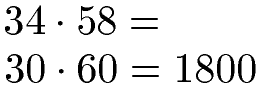
Überschlag Beispiel 2 Multiplikation:
Auch hier noch ein weiteres Beispiel mit einer dreistelligen Zahl und einer zweistelligen Zahl. Die 681 runden wir auf die Hunderterstelle, daher auf 700. Die 89 können wir ebenfalls auf die Hunderterstelle runden. Da die Zehnerstelle eine 8 ist runden wir auf 100 auf. Wir erhalten 7 · 1 = 7 und wir hängen vier Nullen an.
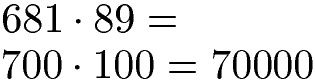
Überschlagen Division und Dezimalzahlen
Mit der Division folgt noch die letzte Grundrechenart. Als erstes Beispiel dienen zwei dreistellige Zahlen welche gerundet und dividiert werden sollen. Im Anschluss noch ein Beispiel mit Dezimalzahlen (Kommazahlen).
Überschlag Division Beispiel 1:
Die dreistelligen Zahlen 412 und 189 werden auf die Hunderterstelle gerundet. Ein Abrunden von 412 auf 400 und ein Aufrunden von 189 auf 200. Durch das Runden erhalten wir die Divisionsaufgabe 400 : 200 = 2.
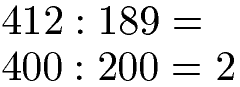
Überschlag Division Beispiel 2 mit Komma:
Sehen wir uns noch eine Divisionsaufgabe mit Komma an. Berechnet werden soll 9,6 : 5,3. Für die Überschlagsrechnung runden wir die Dezimalzahlen auf ganze Zahlen. Eine 6 bei 9,6 nach dem Komma bedeutet aufrunden auf 10. Eine 3 hinter dem Komma bei 5,3 bedeutet abrunden auf 5. Wir lösen die Überschlagsaufgabe 10 : 5 = 2.
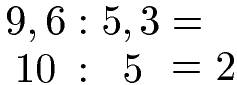
Überschlagen bei Geld und Kommazahlen
Auch bei Geldbeträgen oder dem Rechnen mit Geld werden Dezimalzahlen gerundet. So können Geldbeträge auf ganze Euro gerundet werden um einen Überschlag durchzuführen. Dies bedeutet: Besteht ein Geldbetrag aus Euro und Cent kann auf ganze Eurobeträge gerundet werden. Bei 0 bis 49 Cent wird der Geldbetrag abgerundet, bei 50 bis 99 Cent aufgerundet.
Beispiel: Geld runden und Addition
Gerundet werden sollen die Geldbeträge 8,32 Euro und 4,78 Euro. Diese sollen auf ganze Beträge gerundet werden. Daher werden die 8,32 Euro abgerundet auf 8 Euro. Außerdem werden die 4,78 Euro aufgerundet auf 5 Euro.
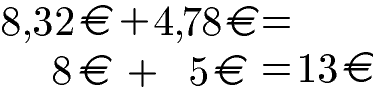
Die Summe aus 8 Euro und 5 Euro ergibt 13 Euro.
Hinweis: Ob bei den Dezimalzahlen eine Einheit (Euro, Dollar, Meter, Sekunde etc.) vorkommt oder nicht spielt für das Runden keine Rolle. Jedoch sollte darauf geachtet werden, dass die Einheiten gleich sind. Also zum Beispiel nicht Meter mit Zentimeter addieren sondern alles auf die gleiche Einheit umrechnen und danach addieren, subtrahieren, multiplizieren oder dividieren.
177 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: