Vektorrechnung: Addition, Subtraktion und Skalarprodukt

In diesem Abschnitt befassen wir uns mit der Vektorrechnung. Dabei zeigen wir euch, wie man die Addition und Subtraktion von Vektoren durchführt so wie das Skalarprodukt bildet.

Die Addition und Subtraktion ist denkbar simpel. Die einzelnen X-Werte und Y-Werte bzw. - sofern vorhanden - auch die Z-Werte werden addiert bzw. von einander abgezogen. Bei dem Skalarprodukt wird es ein klein bisschen komplizierter, aber nicht viel. Beginnen wollen wir jedoch mit der Addition.

Vektorrechnung: Addition

Also hier nun die Addition zur Vektorrechnung. Dabei werden die beiden X-Werte addiert und die beiden Y-Werte addiert. Wäre noch ein Z-Wert vorhanden, würde mit diesem genauso verfahren werden. Hier nun die allgemeine Formel und ein Beispiel:

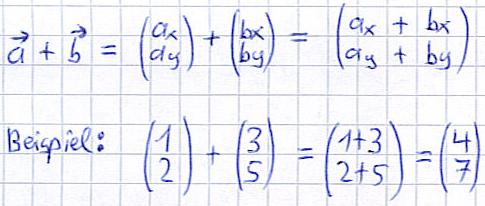
Vektorrechnung: Subtraktion

Die Subtraktion von Vektoren funktioniert sehr ähnlich. Hier werden die beiden X-Werte und Y-Werte voneinander abgezogen. Wäre noch ein Z-Wert vorhanden, würde man diesem ebenso verfahren. Hier wieder die allgemeine Schreibweise und ein Beispiel.

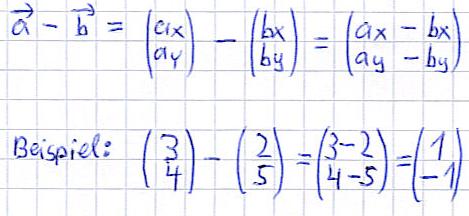
Skalarprodukt, Orthogonal, Senkrecht

Kümmern wir uns nun um das Skalarprodukt von zwei Vektoren. Dazu erneut die allgemeine Schreibweise sowie ein Beispiel, welches jedoch nicht mit dem Z-Wert arbeitet ( Wäre noch ein Z-Wert vorhanden, würde damit genauso verfahren werden ):

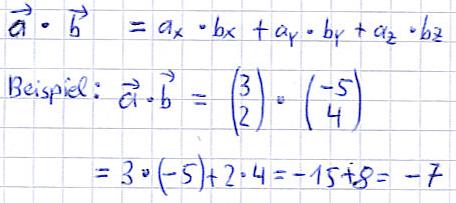
Wir haben in dem Beispiel -7 als Lösung raus bekommen. Wäre eine 0 ( Null ) als Ergebnis ausgerechnet worden, würden die beiden Vektoren senkrecht aufeinander stehen. Man bezeichnet dies auch als Orthogonal.

Merke: Ist das Skalarprodukt zweier ( vom Nullvektor verschiendenen ) Vektoren Null, stehen die beiden Vektoren senkrecht ( = orthogonal ) aufeinander.

Links:

• Zur Vektor-Übersicht
• Zur Mathematik-Übersicht