Würfel Wahrscheinlichkeit / Stochastik

Mit dem Würfel aus Sicht der Wahrscheinlichkeitsrechnung / Stochastik befassen wir uns in diesem Artikel. Dies wird vor allem durch das Vorrechnen einiger Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Ein Würfel kennt eigentlich schon jeder aus dem realen Leben. Die meisten Würfel haben sechs verschiedene Seiten, die mit den Zahlen von 1 bis 6 durchnummeriert werden. Der prinzipielle Aufbau eines Würfel sieht wie folgt aus.

Sofern an dem Würfel nichts manipuliert wurde bzw. bei dessen Herstellung nichts schief gelaufen ist, ist die Wahrscheinlichkeit die Zahl 1 zu würfeln genauso groß wie eine der anderen Zahlen zu Würfeln. Und damit sind wir auch schon Mitten im Thema Stochastik/Wahrscheinlichkeit.

Baumdiagramm Würfel

Beginnen wir zunächst mit Berechnungen der Wahrscheinlichkeiten für einen Würfel, der völlig in Ordnung ist. Die Wahrscheinlichkeit für alle Zahlen auf dem Würfel - also das Würfeln dieser - ist gleich groß. Der Würfel hat sechs Seiten, damit ist die Wahrscheinlichkeit die Zahl 1 zu Würfeln ein Sechstel ( 1/6 ) bzw. bei der Zahl 5 ist diese ebenfalls ein Sechstel ( 1/6 ). So etwas zeichnet man in der Mathematik oftmals in ein Baumdiagramm ein. Für einen Wurf mit einem Würfel mit sechs Seiten sieht ein Baumdiagramm so aus.

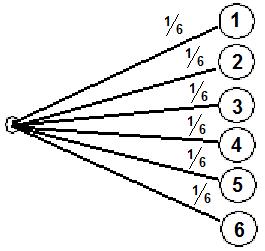
Die Wahrscheinlichkeit für alle Zahlen ist also gleich groß. Dies kann man aus der eben gezeigten Grafik entnehmen. Und damit kann man nun arbeiten, was mit den folgenden Beispielen verdeutlicht werden soll:

1. Wie groß ist die Wahrscheinlichkeit die Zahl 3 zu würfeln? Lösung: Die Wahrscheinlichkeit beträgt 1/6.
2. Wie groß ist die Wahrscheinlichkeit die Zahl 2 zu würfeln? Lösung: Die Wahrscheinlichkeit beträgt 1/6.
3. Wie groß ist die Wahrscheinlichkeit eine 1 oder 3 zu würfeln? Lösung: Die Wahrscheinlichkeit eine 1 zu würfeln beträgt 1/6, ebenso ist die Wahrscheinlichkeit eine 3 zu würfeln ebenfalls 1/6. Von den sechs Seiten stellen also zwei Seiten das gewünschte Ergebnis dar. Damit beträgt die Gesamtwahrscheinlichkeit 2/6.
4. Wie groß ist die Wahrscheinlichkeit eine gerade Zahl zu würfeln? Lösung: Die Zahlen 2, 4 und 6 sind gerade Zahlen. Somit sind 3 der 6 Würfelseiten mit geraden Zahlen versehen. Damit beträgt die Wahrscheinlichkeit 3/6.
5. Wie groß ist die Wahrscheinlichkeit eine ungerade Zahl zu würfeln? Lösung: Die Zahlen 1, 3 und 5 sind ungerade Zahlen. Somit sind 3 der 6 Würfelseiten mit ungeraden Zahlen versehen. Damit beträgt die Wahrscheinlichkeit 3/6.

In den bisherigen Beispielen wurde der Würfel nur einmal geworfen und die Wahrscheinlichkeit berechnet. Was passiert denn aber nun, wenn man mehrfach würfelt? Wie groß wäre also die Wahrscheinlichkeit zweimal am Stück eine sechs zu Würfel oder zweimal in Folge keine 3 zu würfeln? Dazu erweitern wir das Baumdiagramm um auch einen zweiten Wurf abzudecken. Da sich am Würfel nichts ändert, sieht dabei die zweite Stufe genauso aus wie die erste. Aus Platzgründen wird dieses Baumdiagramm etwas gekürzt dargestellt.

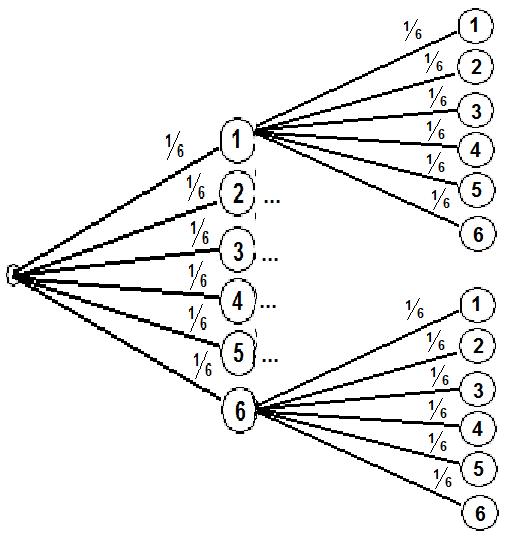
Um nun die Wahrscheinlichkeiten für zwei Würfe zu ermitteln, muss man die Wahrscheinlichkeiten des ersten Versuchs und des zweiten Versuchs multiplizieren. Auch hier einige Beispiele:

1. Wie groß ist die Wahrscheinlichkeit erst eine 1 und dann eine 6 zu Würfeln. Lösung: Diese Wahrscheinlichkeit im ersten Versuch eine 1 zu würfeln beträgt 1/6. Im zweiten Versuch eine 6 zu würfeln ist ebenfalls mit 1/6 anzusetzen. Und multipliziert man diese beiden Brüche erhält man die Wahrscheinlichkeit zu 1/6 · 1/6 = 1/36
2. Wie groß ist die Wahrscheinlichkeit erst eine 6 zu würfeln und dann keine 3 zu würfeln? Lösung: Diese ist im ersten Versuch für eine 6 mit 1/6 anzugeben. Die Wahrscheinlichkeit im zweiten Versuch keine 3 zu würfeln beträgt 5/6. Die Gesamtwahrscheinlichkeit liegt damit bei 1/6 · 5/6 = 5/36.

Links:

• Zur Mathematik-Übersicht