Würfelnetze

Mit den Würfelnetzen befassen wir uns in diesem Artikel. Dabei sollen vor allem Beispiele zum besseren Verständnis dienen. Dieser Artikel gehört zu unserem Bereich Mathematik Grundschule.

In der Mathematik stellt man oftmals Körper als Schrägbilder dar. Man sieht damit eine dreidimensionale Darstellung eines Körpers. Im nun folgenden Beispiel seht ihr einen Würfel, welcher als Schrägbild zu sehen ist. Zur Erinnerung: Ein Würfel ist ein geometrischer Körper, der von sechs zueinander kongruenten Quadraten begrenzt wird. Zum Bild:

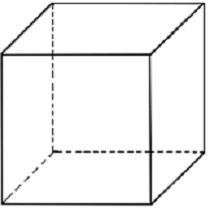
Darüber hinaus kann man Würfel auch als Würfelnetze darstellen. Hinter der folgenden Grafik versteckt sich ebenfalls ein Würfel, dieses mal aber als Würfelnetz dargestellt. Dabei werden die einzelnen Seiten auf dem "Boden ausgebreitet". Man muss nun dieses Würfelnetz zusammenfalten, um den kompletten Würfel zu erhalten. Es folgen zwei Beispiele für solche Würfelnetze:

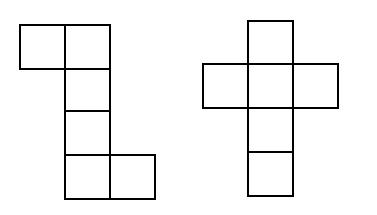
Um zu erkennen, ob es sich wirklich um ein Würfelnetz handelt oder nicht, gibt es zwei verschiedene Möglichkeiten:

1. Man zeichnet das Würfelnetz auf einem Blatt Papier, schneidet dieses am äußeren Rand aus ( also die Begrenzung des Würfelnetzes ) und setzt es zusammen. Wenn es sich dabei um ein Würfelnetz handelt, lässt sich das Blatt Papier mit etwas Geschick auch zu einem Würfel zusammensetzen.
2. Man setzt das Netz im Kopf zusammen und schaut, ob alles passt.  Ein kleiner Trick kann sofort angesetzt werden: Existieren keine 6 Flächen, so kann man daraus gar nicht erst ein Würfel herstellen.

Als Vorbereitung auf eine Klausur empfiehlt es sich nun, entsprechende Aufgaben und Übungen zu Würfelnetzen zu lösen. Mit der Zeit bekommt man dann in aller Regel einen Blick dafür, wie man den Würfel zusammensetzen muss. Außerdem wird man mit etwas Übung in der Regel auch schneller und man kommt in Klausuren nicht so schnell in Zeitnot.

Links:

• Würfelnetze Aufgaben / Übungen
• Zur Mathematik-Übersicht