Zylinder Formeln

Mit den Formeln für den Zylinder befassen wir uns in diesem Artikel. Dazu geben wir euch sowohl die passende Formel als auch ein Beispiel an. Dieser Artikel gehört zu unserem Bereich Mathematik.

Zunächst sollten wir erst einmal kurz klären, was ein Zylinder überhaupt ist. Ein Zylinder ist laut der allgemeinen Definition von zwei parallelen, ebenen Flächen (Grund- und Deckfläche) und einer Mantel- bzw. Zylinderfläche, die von parallelen Geraden gebildet wird, begrenzt. Die folgende Grafik zeigt euch wie so ein Zylinder aussieht. Man beachte auch den Radius und die Höhe dabei.

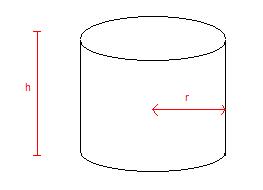
Zylinder Formel: Oberfläche berechnen

Um die Oberfläche eines Zylinders zu berechnen, benötigt man den Radius "r" des Zylinders sowie dessen Höhe "h". Die Formel zur Berechnung der Zylinderoberfläche "A" lautet dann wie folgt:

• A = 2 · π · r · ( r + h )

Beispiel: Oberfläche Zylinder:

Der Radius eines Zylinders beträgt 2 Meter, die Höhe liegt bei 3 Metern. Welchen Oberflächeninhalt hat der Zylinder?

Lösung: Dem Text entnehmen wir die Angaben r = 2m und h = 3m. Diese Werte setzen wir in die Formel ein.

• A = 2 · 3,14159 · 2m · ( 2m + 3m )
• A = 12, 566m · ( 5m )
• A = 62,83m²

Die Oberfläche des Zylinders beträgt demnach 62,83m².

Zylinder Formel: Volumen berechnen

In diesem Abschnitt berechnen wir das Volumen eines Zylinders.  Auch hier benötigen wir den Radius "r" und die Höhe "h" des Zylinders. Das Volumen umfasst dann die Kreisfläche am Boden multipliziert mit der Höhe. Damit lautet die Formel dann:

• V = π · r² · h
  

Beispiel: Volumen Zylinder

Der Radius des Zylinders sei 3cm, die Höhe 4cm. Wie groß ist dann das Volumen? Die Lösung lautet:

• V = π · (3cm)² · 4cm
• V = 113,097cm³

Grundfläche und Mantelfläche des Zylinders

Auch zwei weitere Formeln sollen hier noch angegeben werden. Mit der einen kann man die Mantelfläche "M" berechnen, die andere dient zur Berechnung der Grundfläche "G".

• M = 2 · π · r · h
• G = π · r²

Links:

• Zur Mathematik-Übersicht