Kreisbewegung und Zentripetalkraft (Physik)

Die Kreisbewegung und die Zentripetalkraft sind Thema in diesem Artikel. Dabei erklären wir euch wichtige Begriffe, worum es sich handelt und wie man einige Berechnungen mit den entsprechenden Formeln durchführt.

Jeder kennt eine Kreisbewegung, zum Beispiel von einem Karussell. Wer sich hinsetzt, wird über eine längere Zeit mit gleicher Geschwindigkeit im Kreis gefahren. In der Physik wird solch eine Kreisbahn oftmals wie folgt dargestellt (die Begriffe erklären wir im Anschluss):

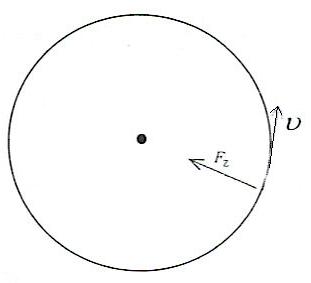
Kreisbewegung Definitionen

Bevor ich euch hier ein paar Formeln vorknalle, solltet ihr erst einmal ein paar Definitionen zur Kreisbewegung kennen. Dabei sind:

• "v" ist die Bahngeschwindigkeit
• "T" ist die Periode, also die Zeit für einen Umlauf des Objektes
• "f" ist die Frequenz, dies sind die Umläufe des Objektes pro Sekunde
• "ω" ist die Kreisfrequenz, der umlaufende Winkel pro Zeit im Bogenmaß (Formel folgt noch)

Formeln zur Kreisbewegung

Kreisfrequenz berechnen:

• Formel: ω = 2 · π · f
• "ω" ist die Kreisfrequenz pro Sekunde [ 1/s ]
• "π" ist die Kreiszahl, π=3,14159
• "f" ist die Frequenz pro Sekunde [ 1/s ]

Geschwindigkeit berechnen:

• Formel: v = r ·  ω
• "v" ist die Geschwindigkeit in Meter pro Sekunde [ m / s ]
• "r" ist der Radius des Kreises in Metern [ m ]
• "ω" ist die Kreisfrequenz pro Sekunde [ 1 / s ]

Beschleunigung berechnen:

• Formel: a = v² : r
• "a" ist die Beschleunigung in Meter pro Sekunde-Quadrat [ m / s² ]
• "v" ist die Geschwindigkeit in Meter pro Sekunde [ m / s ]
• "r" ist der Radius des Kreises in Meter [ m ]

Zentripetalkraft

Bei einer gleichförmigen Kreisbewegung wirkt auf den Körper stets eine Kraft, die immer zum Kreismittelpunkt zeigt. Diese Kraft wird als Zentripetalkraft bezeichnet.

Zentripetalkraft berechnen:

• Formel: F_Z = m · v² : r
• "F_Z" ist die Zentripetalkraft in Newton [ N ]
• "m" ist die Masse des Objektes in Kilogramm [ kg ]
• "v" ist die Geschwindigkeit in Meter pro Sekunde [ m / s ]
• "r" ist der Radius des Kreises in Meter [ m ]

Beispiele: Zentripetalkraft / Kreisbewegung

Im nun Folgenden wollen wir uns einige Beispiele ansehen, welche den Umgang mit den Formeln demonstrieren.

Beispiel 1: Ein 0.4kg schwerer Körper wird an einer 0.8m langen Schnur auf einer Kreisbahn geschleudert.  Die Frequenz beträgt f = 1.33/s. Welche Kraft wirkt?

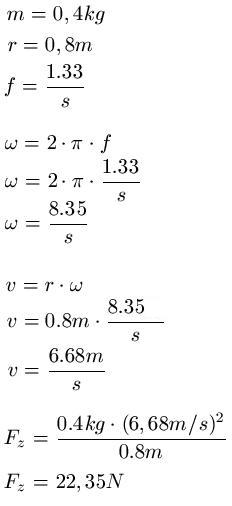
Beispiel 2: Ein 0.4kg schwerer Körper wird an einer 0.8m langen Schnur auf einer Kreisbahn geschleudert.  Die Schnur hält 500N Belastung aus. Bei welcher Umdrehungszahl reißt die Schnur?

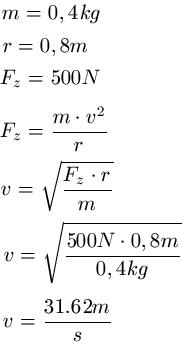
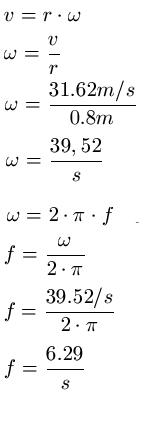
Links:

• Zu den Aufgaben Kreisbewegung / Zentripetalbeschleunigung
• Zurück zur Mechanik-Übersicht
• Zurück zur Physik-Übersicht