Werner Heisenberg Unschärferelation

Mit der Heisenbergschen Unschärferelation befassen wir uns in diesem Artikel. Dabei erklären wir euch, was man unter der Heisenbergschen Unschärferelation zu verstehen hat und wie man damit rechnet ( inklusive Beispiel ). Dieser Artikel gehört zum Bereich Grundlagen der Quantenphysik.

Werner Karl Heisenberg lebte von 1901 - 1976 und war einer der bedeutendsten Physiker des 20. Jahrhunderts und auch Nobelpreisträger. Er formulierte 1927 die nach ihm benannte Heisenbergsche Unschärferelation, welche bis heute eine der fundamentalen Aussagen der Quantenmechanik ist. Diese besagt, dass einer Materiewelle nie gleichzeitig ein Ort und ein Impuls mit beliebiger Genauigkeit zugeordnet werden kann. Jede Steigerung der Genauigkeit bei der Ortsbestimmung eines Teilchens geht zu Lasten der Genauigkeit der Impulsbestimmung und umgekehrt.

Heisenberg Unschärferelation berechnen

Es gibt eine Gleichung für die Heisenberg-Unschärferelation bzw. Heisenberg Unbestimmtheitsrelation. Diese lautet wie folgt:

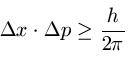
Je nach Literatur wird manchmal auch folgende Gleichung verwendet (Siehe Hinweis weiter unten):

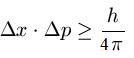
Dabei ist:

• "Δx" ist die Unsicherheit der Ortskoordinate in Meter [ m ]
• "Δp" ist die Unsicherheit der Impulsangabe in Kilogramm-Meter pro Sekunde [ kgm/s ]
• "h" ist das Plancksche Wirkungsquantum in Joule-Sekunde [ Js ]

Es gilt:

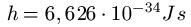
Wichtiger Hinweis: Ich erhalte E-Mails in denen andere Ungleichungen für die Heisenbergsche Unschärferelation genannt werden. Welche Ungleichung zu verwenden ist, hängt von den Umständen ab. Wer hier unsicher ist, sollte den Lehrer bzw. Prof Fragen oder im entsprechenden Schulbuch / Skript / Laborbeschreibung oder der Aufgabe nachlesen!

Erläuterung:

Der Gleichung der Heisenbergschen Unschärferelation kann man entnehmen, dass je genauer die Lagekoordinate angegeben wird, desto größer ist die Unschärfe des Impulses und umgekehrt. Im Gegensatz zur klassischen Physik können beide Angaben nicht mit beliebiger Genauigkeit erfasst werden.

Beispiel:

Die Unschärfe für eine Ortsbestimmung soll 1/10 des Atomdurchmessers eines Wasserstoff-Atoms betragen, sprich Δx = 10^-11 m. Damit beträgt die Unschärfe des Impulses:

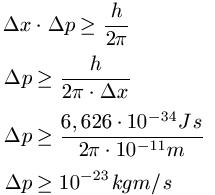
Links:

• Zur Quantenphysik-Übersicht
• Zur Physik-Übersicht