Thermischer Wirkungsgrad

Mit dem thermischen Wirkungsgrad befassen wir uns in diesem Artikel. Dabei wird erklärt, was man unter dem thermischen Wirkungsgrad versteht und wie man diesen berechnet. Dieser Artikel gehört zum Bereich Thermodynamik.

Zunächst sollten wir einen kurzen Blick auf den normalen Wirkungsgrad werfen. Im Anschluss sehen wir uns den thermischen Wirkungsgrad an. Bei allen Maschinen tritt Reibung auf. Somit ist die von der Maschine verrichtete Arbeit um den zur Überwindung der Reibung verbrauchten Arbeitsbetrag kleiner als die Arbeit, welche der Maschine zugeführt wird. Unter dem Wirkungsgrad versteht man das Verhältnis der verrichteten Arbeit zur zugeführten Arbeit.  Die Formel sieht dabei wie folgt aus:

Allgemeiner Wirkungsgrad:

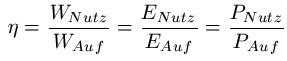
Dabei ist:

• "η" der Wirkungsgrad, Einheitenlos
• "W_Nutz, E_Nutz, P_Nutz" ist die verrichtete Arbeit, Energie oder Leistung
• "W_Auf, E_Auf, P_Auf" ist die zugeführte Arbeit, Energie oder Leistung

Der Wirkungsgrad kann nur zwischen 0% und 100% bzw. zwischen 0 und 1 liegen. Ein Wirkungsgrad größer als 1 bzw. 100% ist physikalisch unmöglich.

Thermischer Wirkungsgrad berechnen

Der thermische Wirkungsgrad berechnet sich sehr ähnlich. Zu dessen Berechnung kann man die folgende Formel einsetzen:

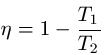
Dabei ist:

• "η" der Wirkungsgrad, Einheitenlos
• "T₁" ist die Abgastemperatur in Kelvin [ K ]
• "T₂"  ist die Ausgangstemperatur in Kelvin [ K ]

Beispiel:

Bei einer Dampfmaschine sei die Anfangstemperatur des Wasserdampfes bei T₂ = 673K. Die Kondensatortemperatur kann zu T₁ = 323K angenommen werden. Damit berechnet sich der Wirkungsgrad zu:

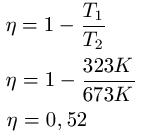
Links:

• Zur Thermodynamik-Übersicht
• Zur Physik-Übersich