Gruppenschaltung
Geschrieben von: Dennis RudolphDonnerstag, 28. Dezember 2017 um 18:51 Uhr
In einem Stromkreis finden sich oft viele Widerstände vor, die in Reihe oder Parallel liegen. Wie man diese sinnvoll zusammenfasst, um anschließend das Ohmsche Gesetz anwenden zu können, lernt ihr in diesem Artikel zur Gruppenschaltung.
Eines vorweg: Wer noch nicht weiß, was man unter den Begriffen Strom, Spannung und Widerstand zu verstehen hat oder das Ohmsche Gesetz noch nicht kennt, sollte sich erst einmal die folgenden Artikel durchlesen. Zu dem ist es gut, noch die Parallelschaltung bzw. Serienschaltung von Widerständen zu kennen. Ansonsten wird es schwierig dem weiteren Artikel noch zu folgen.
- Elektrotechnik: Strom, Spannung und Widerstand
- Elektrotechnik: Das Ohmsche Gesetz
- Elektrotechnik: Serienschaltung Widerstand
- Elektrotechnik: Parallelschaltung Widerstand
Gruppenschaltung von Widerständen
An einfachen Beispielen möchte ich euch nun zeigen, wie man eine so genannte Gruppenschaltung berechnet. Unter einer Gruppenschaltung versteht man eine elektronische Schaltung, bei der Widerstände sowohl als Reihenschaltung, wie auch als Parallelschaltung vorkommen. Werft dazu einen Blick auf das folgende Beispiel.
Beispiel 1:
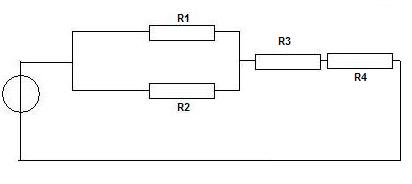
Wie man sehen kann, liegen die Widerstände R1 und R2 parallel zu einander. Die Widerstände R3 und R4 hingegen liegen als Reihenschaltung vor. Mit dem Wissen zur Reihenschaltung und Parallelschaltung kann man diese nun zusammen fassen. Wir erhalten dadurch die Ersatz-Widerstände RVorne und RHinten. Dies sieht dann wie folgt aus:
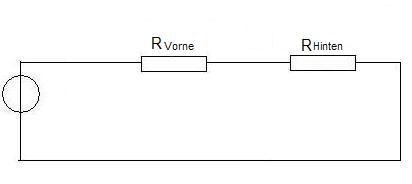
Die Berechnung für RVorne und RHinten sehen wie folgt aus. Anschließend werden diese beiden in Reihe geschalteten Widerstände wieder zusammen gefasst. Hier die Rechnung:
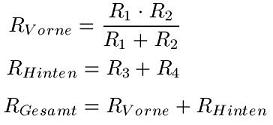
Beispiel 1 mit Zahlen:
Zur besseren Verdeutlichung soll nun das Beispiel noch mit Zahlen gerechnet werden. Für die vier Widerstände setzen wir nun die folgenden Zahlen ein und berechnen damit den Gesamtwiderstand.
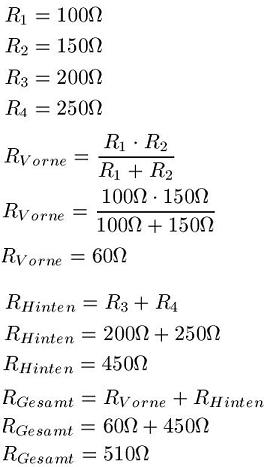
Beispiel 2:
Zeit für ein zweites Beispiel. Hier die Schaltung, deren Gesamtwiderstand berechnet werden soll.
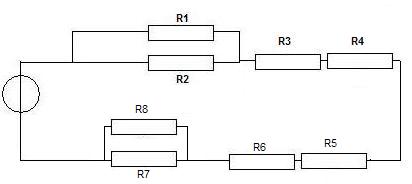
Die Widerstände R1 und R2 sowie R7 und R8 liegen jeweils parallel zueinander. Alle anderen Widerstände liegen in Reihe zueinander. Den Gesamtwiderstand berechnet man somit wie folgt:
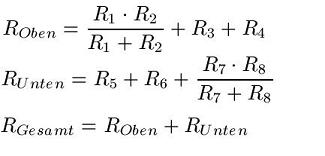
Links: