Ableitung: Produktregel und Quotientenregel (Ableitungsregel)

In diesem Abschnitt befassen wir uns mit dem Ableiten von Funktionen. Dabei zeigen wir euch, wie die Ableitungsregeln "Produktregel" und "Quotientenregel" angewendet werden müssen.

Bevor wir mit der Produktregel und Quotientenregel loslegen, rate ich euch, die beiden vorhergehenden Artikel zur Ableitung zu lesen. Dort wird Grundlagenwissen vermittelt. Wer sich in diesen Bereichen bereits auskennt, kann gleich mit der Ableitungsregel zu Produkten im nächsten Abschnitt starten:

• Ableitung: Grundlagen und Steigung
• Ableitung: Faktorregel und Summenregel

Produktregel

Mit der Faktor- und Summenregel haben wir uns bereits befasst. Nun kommen wir zur Produktregel. Diese wird eingesetzt, wenn ein Produkt abgeleitet werden soll. Es folgt zunächst einmal die Formel. Danach folgen Erklärungen und Beispiele.

Produktregel: Ausführliche Schreibweise

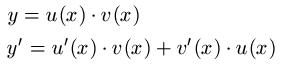
Produktregel: Kurzschreibweise

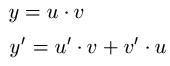
Ihr müsst bei der Funktion oder Gleichung die abgeleitet werden soll einen Teil als u und einen Teil als v bezeichnen. Diesen jeweiligen Teil leitet Ihr ab und setzt diese in die Gleichung von y' ein. Die folgenden Beispiele zeigen euch dies:

Beispiel 1:

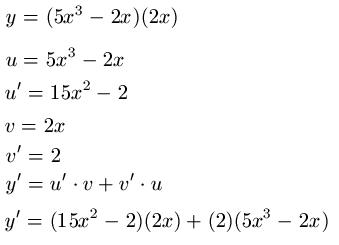
Beispiel 2:

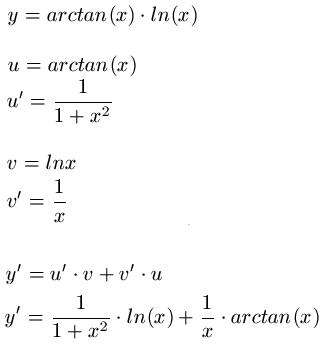
Quotientenregel

Nach der Produktregel, kommen wir nun zur Quotientenregel. Diese kommt zum Einsatz, wenn ihr einen Bruch ableiten wollt. Wie immer zunächst die allgemeine Regel, danach einige Erklärungen und Beispiele.

Quotientenregel: Ausführliche Schreibweise

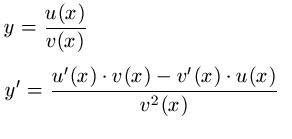
Quotientenregel: Kurzschreibweise

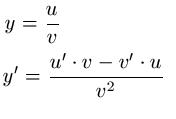
Den Zähler setzt ihr u, den Nenner setzt ihr v. Leitet diese dann beide ab und setzt dies in y' ein. Das folgende Beispiel verdeutlicht dies:

Beispiel 1:

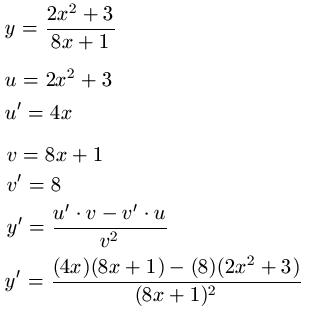
Beispiel 2:

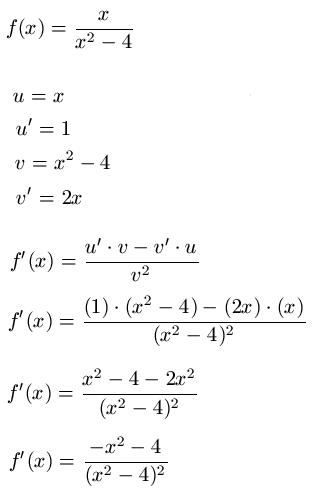
Links:

• Produktregel Aufgaben / Übungen
• Zur Formelsammlung Ableitung
• Zurück zur Ableitung-Übersicht
• Zur Mathematik-Übersicht