Ableitung von ln x

Mit der Ableitung von ln x befassen wir uns in diesem Artikel. Dabei erklären wir euch die Ableitungsregel "Kettenregel" und liefern euch eine Reihe an Beispielen. Dieser Artikel gehört zum Bereich Mathematik.

Im Internet werden ln-Funktionen verschieden dargestellt bzw. geschrieben. In vielen Foren finden sich so zum Beispiel Einträge wie "Ableitung ln x, Ableitung ln 1 x, Ableitung ln 2, x lnx Ableitung etc.. Für eine bessere Übersicht verwenden wir hier jedoch Latex zur Darstellung. Zunächst werfen wir jedoch einen Blick auf die Kettenregel, die zur Ableitung einer ln-Funktion benötigt wird.

Ableitung ln-Funktion durch Kettenregel

Mit den bisherigen Ableitungsregeln ( Summenregel, Faktorregel etc. ) ist es möglich, einfache Funktionen abzuleiten. Problematisch wird es jedoch, wenn zusammengesetzte oder gar verschachtelte Funktionen abgeleitet werden müssen.  Um Funktionen wie zum Beispiel ln (2x + 5) abzuleiten, muss die Kettenregel eingesetzt werden. Man greift dabei auf eine so genannte Substitution zurück. Was genau es damit auf sich hat, erkläre ich euch noch. Zunächst jedoch ein kleiner Merksatz.

Kettenregel: Die Ableitung einer zusammengesetzten ( verketteten ) Funktion erhält man als Produkt aus äußerer und innerer Ableitung.

Viele Schüler haben zu Beginn größere Schwierigkeiten diese Regel anzuwenden. Grund: Es gehört etwas Erfahrung dazu, um zu sehen, dass die Kettenregel überhaupt angewendet werden muss. Im nun Folgenden stelle ich euch einige typische Beispiele vor, bei der durch Anwendung der Kettenregel die Ableitung von ln x oder ähnlichen Funktionen gebildet wird. Dabei wird zunächst der Rechenweg gezeigt, darunter finden sich Erläuterungen.

Beispiel 1: Ableitung von ln x

Beginnen wir mit der Ableitung der Funktion ln x. Deren Lösung entnimmt man einer Tabelle ( und benötigt noch keine Kettenregel ).

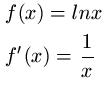
Beispiel 2: Ableitung von ln 3x

Um die Ableitung von ln 3x zu bestimmen, ist der Einsatz der Kettenregel nötig. Dabei ermitteln wir die Ableitungen der äußeren und inneren Funktion und multiplizieren diese miteinander.

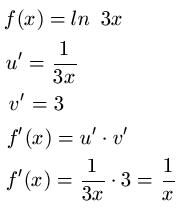
Beispiel 3: Ableitung von ln ( 2x + 5 )

Um die Ableitung von ln ( 2x + 5 ) zu bestimmen, ist der Einsatz der Kettenregel nötig. Dabei ermitteln wir die Ableitungen der äußeren und inneren Funktion und multiplizieren diese miteinander.

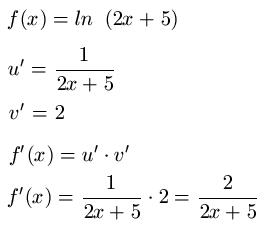
Links:

• Zur Ableitung-Übersicht
• Zur Mathematik-Übersicht