Betrag eines Vektors

Wie man den Betrag eines Vektors berechnet, lernt ihr in diesem Artikel der Mathematik. Dabei betrachten wir sowohl den Betrag eines ebenen, wie auch den Betrag eines räumlichen Vektors.

Bevor wir mit der Berechnung des Betrags eines Vektors starten, folgt noch ein kurzer Hinweis: Ihr solltet wissen, was ein Vektor ist und den Satz des Pythagoras kennen. Wem dies noch nicht klar ist, der möge bitte erst einmal die folgenden Artikel lesen. Alle anderen können gleich mit dem nächsten Absatz fortfahren.

• Ebener Vektor und räumlicher Vektor
• Satz des Pythagoras

Betrag eines Vektors: Einleitung

Der Betrag eines Vektors entspricht der Länge dieses Vektors. Man weiß nach der Betragsbildung somit, welche Streckenlänge dieser Vektor in der Ebene oder im Raum hat. Die Idee dafür entstammt dem Satz des Pythagoras. Die folgende Grafik zeigt euch dies:

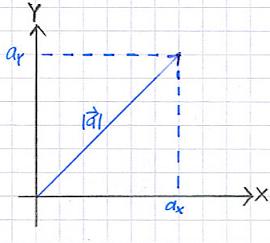
Zur Erinnerung: Die Längen a_x und a_y stellen die Katheten des Dreiecks dar, der Betrag des Vektors entspricht der Hypotenuse. Kennt man die Längen der beiden Katheten, kann man mit dem Satz des Pythagoras die Länge der Hypotenuse berechnen.

Betrag eines ebenen Vektors

Um die Länge eines ebenen Vektors zu bestimmen, berechnen wir dessen Betrag. Es folgt zunächst die allgemeine Formel um diese Berechnung durchzuführen. Im Anschluss erhaltet ihr ein Beispiel.

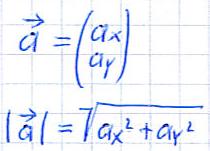
Beispiel:

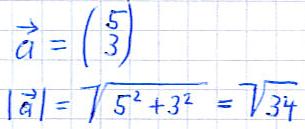
Betrag eines räumlichen Vektors

Um die Länge eines räumlichen Vektors zu bestimmen, berechnen wir dessen Betrag. Es folgt zunächst die allgemeine Formel um diese Berechnung durchzuführen. Im Anschluss erhaltet ihr auch ein Beispiel.

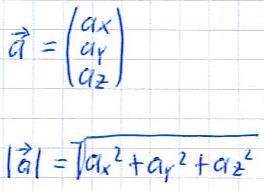
Beispiel:

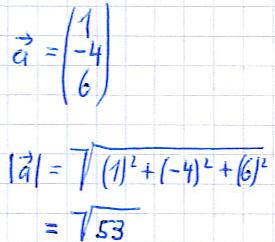
Links:

• Zur Vektor-Übersicht
• Zur Mathematik-Übersicht